
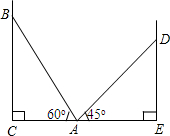
 在两面墙之间有一个低端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=$\sqrt{18}$m.
在两面墙之间有一个低端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点,已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=$\sqrt{18}$m.分析 (1)在Rt△ADE中,运用勾股定理可求出梯子的总长度,然后利用勾股定理求得AC的长,从而求得线段CE的长;
(2)在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.
解答 解:(1)在Rt△DAE中,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°,AE=DE=3$\sqrt{2}$m,
∴AD2=AE2+DE2=36,
∴AD=6,即梯子的总长为6m.
∴AB=AD=6m.
在Rt△ABC中,∵∠BAC=60°,
∴∠ABC=30°,
∴AC=$\frac{1}{2}$AB=3m,
∴CE=AC+AE=(3+3$\sqrt{2}$)m;
(2)BC2=AB2-AC2=62-32=27,
∴BC=3$\sqrt{3}$m,
∴点B到地面的垂直距离BC的大小3$\sqrt{3}$m.
点评 本题考查了勾股定理的应用,如何从实际问题中整理出直角三角形并正确运用勾股定理是解决此类题目的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≠1-$\sqrt{5}$ | B. | x≠$\frac{1-\sqrt{5}}{2}$ | C. | x≠-1±$\sqrt{5}$ | D. | x≠$\frac{-1±\sqrt{5}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com