
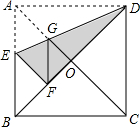
 如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB、AC于点E,G,连接GF,下列结论:①AE=AG;②AB=($\sqrt{2}$+1)AE;③GF∥AB;④BE=2OG.则其中正确的结论个数为( )
如图,在正方形ABCD中,对角线AC、BD交于点O,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB、AC于点E,G,连接GF,下列结论:①AE=AG;②AB=($\sqrt{2}$+1)AE;③GF∥AB;④BE=2OG.则其中正确的结论个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据正方形的性质得到∠DAC=∠ADB=∠ABD=45°,由折叠的性质得到∠ADE=∠FDE=$\frac{1}{2}$∠ADB=22.5°,根据等腰三角形的判定定理得到AE=AG,即①正确;设EF=x,则AE=x,BE=$\sqrt{2}$EF=$\sqrt{2}$x,AB=AE+BE=($\sqrt{2}$+1)x,根据三角函数的定义得到AB=($\sqrt{2}$+1)AE;即②正确;根据折叠的性质得到∠FGE=∠AEG,根据平行线的判定得到GF∥AB,即③正确;由上面的解答可得:AE=$\sqrt{2}$x,OG=$\frac{\sqrt{2}}{2}$x,于是得到BE=2OG,即④正确.
解答 解:∵四边形ABCD是正方形,
∴∠DAC=∠ADB=∠ABD=45°,
由折叠的性质可得:∠ADE=∠FDE=$\frac{1}{2}$∠ADB=22.5°,
则∠AEG=90°-∠ADE=67.5°,∠AGE=∠ADE+∠DAC=22.5°+45°=67.5°,
∵∠AGE=∠AEG=67.5°,
∴AE=AG,即①正确;
设EF=x,则AE=x,BE=$\sqrt{2}$EF=$\sqrt{2}$x,AB=AE+BE=($\sqrt{2}$+1)x,
tan∠AGE=tan∠AEG=$\frac{AD}{AE}=\frac{AB}{AE}$=$\sqrt{2}$+1,
∴AB=($\sqrt{2}$+1)AE;即②正确;
∵∠AGE=∠FGE(折叠的性质),∠AGE=∠AEG(①已证),
∴∠FGE=∠AEG,
∴GF∥AB,即③正确;
由上面的解答可得:AE=$\sqrt{2}$x,OG=$\frac{\sqrt{2}}{2}$x,
故可得BE=2OG,即④正确.
综上可得:①②③④正确,共4个.
故选D.
点评 本题考查了翻折变换的知识,综合考查了相似三角形的判定与性质、等腰梯形的判定及正方形的性质,解答本题的关键是熟练掌握各个知识点,将所学知识融会贯通,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
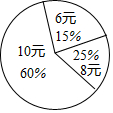 学校食堂午餐供应6元、8元和10元三种价格的盒饭,如图是食堂某月销售三种午餐盒饭数量的统计图,则该月食堂销售午餐盒饭的平均价格为( )
学校食堂午餐供应6元、8元和10元三种价格的盒饭,如图是食堂某月销售三种午餐盒饭数量的统计图,则该月食堂销售午餐盒饭的平均价格为( )| A. | 7.9元 | B. | 8元 | C. | 8.9元 | D. | 9.2元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{a}$ | B. | $\sqrt{\frac{1}{{a}^{2}}}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{-{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 20 | C. | 10 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每人销售台数 | 20 | 17 | 13 | 8 | 5 | 4 |
| 人数 | 1 | 1 | 2 | 5 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com