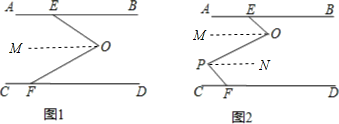
(1)证明:过O作OM∥AB,
∵AB∥CD,
∴AB∥OM∥CD,
∴∠BEO=∠MOE,∠DFO=∠MOF,
∴∠BEO+∠DFO=∠EOM+∠FOM,
即∠EOF=∠BEO+∠DFO.
(2)∠BEO、∠O、∠P、∠PFC会满足的关系式是:∠BEO+∠P=∠O+∠PFC,
解:过O作OM∥AB,PN∥AB,
∵AB∥CD,
∴AB∥OM∥PN∥CD,
∴∠BEO=∠EOM,∠PFC=∠NPF,∠MOP=∠NPO,
∴∠EOP-∠OPF=(∠EOM+∠MOP)-(∠OPN+∠NPF)=∠EOM-∠NPF,
∠BEO-∠PFC=∠EOM-∠NPF,
∴∠BEO-∠PFC=∠EOP-∠OPF,
∴∠BEO+OPF=∠EOP+∠PFC.
(3)解:令折点是1,2,3,4,…,n,
则:∠BEO+∠2+∠4+…=∠1+∠3+∠5+…+∠PFC.
分析:(1)过O作OM∥AB,根据平行线性质推出∠BEO=∠MOE,∠DFO=∠MOF,相加即可求出答案;
(2)过O作OM∥AB,PN∥AB,根据平行线性质求出∠BEO=∠EOM,∠PFC=∠NPF,∠MOP=∠NPO,代入求出即可;
(3)根据(1)(2)总结出规律,即可得出当折点是1,2,3,4,…,n时∠BEO+∠2+∠4+…=∠1+∠3+∠5+…+∠PFC.
点评:本题考查了平行线的性质的应用,解此题的关键是正确作辅助线,并根据证出的结果得出规律,题目比较典型,但是有一定的难度.

 如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
如图1,AB∥CD,EOF是直线AB、CD间的一条折线.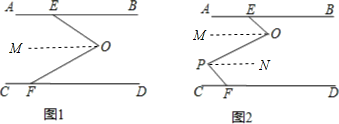


 阅读快车系列答案
阅读快车系列答案