
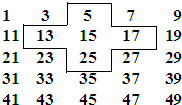
 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.分析 (1)将十字框中的五个数相加即可得出结论;
(2)结合(1)将15替换成a,则可得出结论;
(3)随着十字框移动,上下两数之和为中间数的2倍,左右两数之和为中间数的2倍,由此可得出该规律存在;
(4)设中间的数为x,其它4个数分别为x-10、x-2、x+2、x+10,令其相加等于2015算出x的值,结合数阵数的特点即可得出结论;
(5)若设中间的数为x,其它4个数分别为x-10、x-2、x+2、x+10,令其相加等于2020算出x的值,结合x不能为偶数即可得出结论.
解答 解:(1)∵5+13+15+17+25=75=5×15,
∴十字框中的五个数的和是中间数15的5倍;
(2)由(1)可知:若中间数为a,则十字框中五个数之和5a;
(3)若将十字框中上下左右移动,则上下两数之和为中间数的2倍,左右两数之和为中间数的2倍,
∴5个数的和仍是中间数的5倍;
(4)能.理由如下:
设中间的数为x,其它4个数分别为x-10、x-2、x+2、x+10,
5个数之和为x-10+(x-2)+x+(x+2)+(x+10)=5x=2015,
解得x=403,
∵403为奇数,且在数阵的第400行第二列,
∴存在五个数之和等于2015,五个数分别为:393、401、403、405、413.
(5)不能.理由如下:
若设中间的数为x,其它4个数分别为x-10、x-2、x+2、x+10,
5个数之和为x-10+(x-2)+x+(x+2)+(x+10)=5x=2020,
解得x=404,
∵404为偶数,不在此数阵中,故不能.
点评 本题考查了一元一次方程的应用以及规律型中数字的变化,根据十字框中5个数的特点找出十字框中的五个数的和是中间数的5倍是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
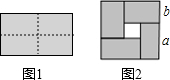 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )| A. | a2-b2 | B. | 2ab | C. | (a+b)2 | D. | (a-b)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com