
【题目】已知正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边分别交CB、
绕点A顺时针旋转,它的两边分别交CB、![]() 或它们的延长线
或它们的延长线![]() 于点M、N,当
于点M、N,当![]() 绕点A旋转到
绕点A旋转到![]() 时
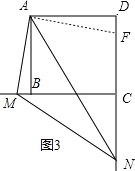
时![]() 如图
如图![]() ,则
,则

![]() 线段BM、DN和MN之间的数量关系是______;
线段BM、DN和MN之间的数量关系是______;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 时
时![]() 如图
如图![]() ,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 如图
如图![]() 的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
【答案】(1)![]() (2)猜想:
(2)猜想:![]() ,详见解析;(3)
,详见解析;(3)![]() 详见解析.
详见解析.
【解析】
(1)连接AC,交MN于点G,则可知AC垂直平分MN,结合∠MAN=45°,可证明△ABM≌△AGM,可得到BM=MG,同理可得到NG=DN,可得出结论;
(2)在MB的延长线上,截取BE=DN,连接AE,则可证明△ABE≌△ADN,可得到AE=AN,进一步可证明△AEM≌△ANM,可得结论BM+DN=MN;
(3)在DC上截取DF=BM,连接AF,可先证明△ABM≌△ADF,进一步可证明△MAN≌△FAN,可得到MN=NF,从而可得到DN-BM=MN.
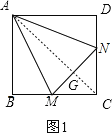
![]() 如图1,连接AC,交MN于点G,
如图1,连接AC,交MN于点G,
![]() 四边形ABCD为正方形,
四边形ABCD为正方形,
![]() ,且
,且![]() ,
,
![]() ,且AC平分
,且AC平分![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
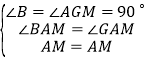 ,
,
![]() ≌
≌![]() ,
,
![]() ,同理可得
,同理可得![]() ,
,
![]() ,
,
故答案为:![]() ;
;
![]() 猜想:
猜想:![]() ,证明如下:
,证明如下:
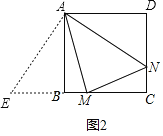
如图2,在MB的延长线上,截取![]() ,连接AE,
,连接AE,
在![]() 和
和![]() 中,
中,
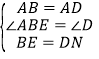 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
又![]() ,
,
![]() ;
;
![]() ,证明如下:
,证明如下:
如图3,在DC上截取![]() ,连接AF,
,连接AF,
![]() 和
和![]() 中,
中,
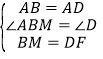 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
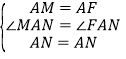 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,已知直线EF//GH,且EF和GH之间的距离为1,小明同学制作了一个直角三角形硬纸板ACB,其中∠ACB=90°,∠BAC=60°,AC=1.小明利用这块三角板进行了如下的操作探究:
(1)如图1,若点C在直线EF上,且∠ACE=20°,求∠1的度数;
(2)若点A在直线EF上,点C在EF和GH之间(不含EF、GH上),边BC、AB与直线GH分别交于点D和点K.
①如图2,∠AKD、∠CDK的平分线交于点O.在△ABC绕着点A旋转的过程中,∠O的度数是否变化?若不变,求出∠O的度数:若变化,请说明理由;
②如图3,在△ABC绕着点A旋转的过程中,设∠EAK=n°,∠CDK=(4m-3n-10)°,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
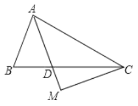
【题目】已知,如图,在△ABC 中,AD 平分∠BAC,AD=AB,CM⊥AD 于 M,请你通过观察和测量,猜想线段 AB、AC 之和与线段 AM 有怎样的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的直角顶点C置于直线l上,AC=BC,现过A.B两点分别作直线l的垂线,垂足分别为点D.E.
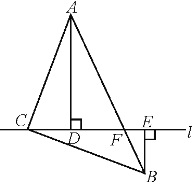
(1)求证:△ACD≌△CBE.
(2)若BE=3,DE=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]()
(1)请直接写出方程![]() 的所有正整数解
的所有正整数解
(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
查看答案和解析>>
科目:初中数学 来源: 题型:
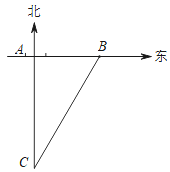
【题目】如图,一艘轮船以30km/h的速度沿既定航线由南向北航行,途中接到台风警报,某台风中心正以10km/h的速度由东向西移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离AB=300km.
(1)如果这艘船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
(3)假设轮船航向不变,轮船航行速度不变,求受到台风影响的时间为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
![]() 求一只A型节能灯和一只B型节能灯的售价各是多少元?
求一只A型节能灯和一只B型节能灯的售价各是多少元?
![]() 工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,当购进A型节能灯m只时,工厂的总费用为w元.
工厂准备购进这两种型号的节能灯共50只,且A型节能灯的数量不多于B型节能灯数量的4倍,当购进A型节能灯m只时,工厂的总费用为w元.
![]() 写出
写出![]() 元
元![]() 与
与![]() 只
只![]() 之间的函数关系式,并写出自变量取值范围;
之间的函数关系式,并写出自变量取值范围;
![]() 如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少?
如何购买A、B型节能灯,可以使总费用最少,且总费用最少是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com