
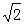 ,P是AC上的一个动点.
,P是AC上的一个动点.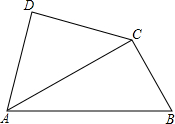
 ,
, ,
,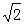 ,
, ;(2)75°;(3)
;(2)75°;(3) ,
,
 ,∠ADF=45°,又PD=BC=
,∠ADF=45°,又PD=BC=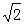 ,即可得到
,即可得到 =
= ,则∠PDF=30°,即可求得∠PDA的度数,当P点位置如图(3)所示时,同(2)可得∠PDF=30°,即可求得结果;
,则∠PDF=30°,即可求得∠PDA的度数,当P点位置如图(3)所示时,同(2)可得∠PDF=30°,即可求得结果; ,再根据平行四边形的面积公式求解即可.
,再根据平行四边形的面积公式求解即可. ,AC=
,AC= ,BC=
,BC=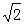 ,四边形ABCD的面积=
,四边形ABCD的面积= ;
;
 ,∠ADF=45°,又PD=BC=
,∠ADF=45°,又PD=BC=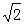 ,
, =
= ,
,
 .
. ,
, =
= .
.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
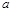 ,其中
,其中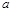 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.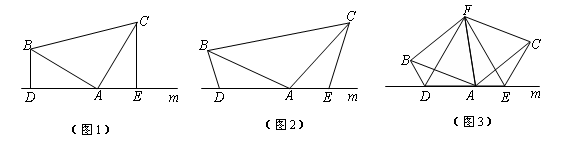
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
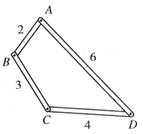
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
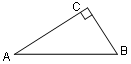
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com