
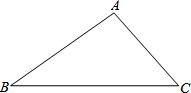
 如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积.
如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积. 分析 过A作AD⊥BC于D,则∠ADC=∠ADB=90°,求出AD=$\frac{1}{2}$AB=12,BD=AB×cos30°=12$\sqrt{3}$,∠BAD=60°,求出∠CAD=45°,求出CD=AD=12,求出BC,根据三角形的面积公式求出即可.
解答 解:
过A作AD⊥BC于D,则∠ADC=∠ADB=90°,
∵∠B=30°,AB=24,
∴AD=$\frac{1}{2}$AB=12,BD=AB×cos30°=12$\sqrt{3}$,∠BAD=60°,
∵∠BAC=105°,
∴∠CAD=45°,
∴∠C=45°=∠CAD,
∴CD=AD=12,
∴BC=BD+CD=12$\sqrt{3}$+12),
∴△ABC的面积是$\frac{1}{2}$BC×AD=$\frac{1}{2}$×(12$\sqrt{3}$+12)×12=72$\sqrt{3}$+72,
即△ABC的面积是72$\sqrt{3}$+72.
点评 本题考查了解再见三角形,等腰三角形的性质,三角形的面积,含30度角的直角三角形的性质的应用,解此题的关键是能构造直角三角形,并进一步求出BC和高AD的长.


科目:初中数学 来源: 题型:解答题
 作图与计算:在所给图中仅用直尺和圆规按要求作图(保留作图痕迹,不写作法)
作图与计算:在所给图中仅用直尺和圆规按要求作图(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A地在B地的正南方向3km处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答:
已知A地在B地的正南方向3km处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,长方形ABCD的长BC为3cm,宽AB为2cm,点E、F是边AD的三等分点,点G、H是边BC的三等分点.现分别以B、G两点为圆心,以2cm长为半径画弧AH和弧EC,则阴影部分的面积为2cm2.
如图,长方形ABCD的长BC为3cm,宽AB为2cm,点E、F是边AD的三等分点,点G、H是边BC的三等分点.现分别以B、G两点为圆心,以2cm长为半径画弧AH和弧EC,则阴影部分的面积为2cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
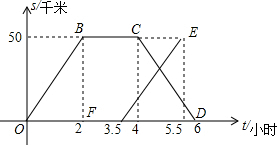 为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)
为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m.
如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com