
”¾ĢāÄæ”æČē¹ūÅ×ĪļĻß![]() µÄ¶„µćŌŚĪļĻß
µÄ¶„µćŌŚĪļĻß![]() ÉĻ£¬Å×ĪļĻß
ÉĻ£¬Å×ĪļĻß![]() µÄ¶„µćŅ²ŌŚĪļĻß
µÄ¶„µćŅ²ŌŚĪļĻß![]() ÉĻŹ±£¬ÄĒĆ“ĪŅĆĒ³ĘÅ×ĪļĻß
ÉĻŹ±£¬ÄĒĆ“ĪŅĆĒ³ĘÅ×ĪļĻß![]() Óė
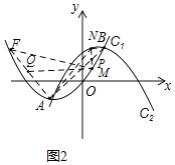
Óė![]() ”°»„ĪŖ¹ŲĮŖ”±µÄÅ×ĪļĻߣ®ČēĶ¼1£¬ŅŃÖŖÅ×ĪļĻß
”°»„ĪŖ¹ŲĮŖ”±µÄÅ×ĪļĻߣ®ČēĶ¼1£¬ŅŃÖŖÅ×ĪļĻß![]() £ŗ
£ŗ![]() Óė
Óė![]() £ŗ
£ŗ![]() ŹĒ”°»„ĪŖ¹ŲĮŖ”±µÄĪļĻߣ¬µć
ŹĒ”°»„ĪŖ¹ŲĮŖ”±µÄĪļĻߣ¬µć![]() ·Ö±šŹĒÅ×ĪļĻß
·Ö±šŹĒÅ×ĪļĻß![]() £¬
£¬![]() µÄ¶„µć£¬Å×ĪļĻß
µÄ¶„µć£¬Å×ĪļĻß![]() ¾¹żµć
¾¹żµć![]() £®
£®
£Ø1£©Ö±½ÓŠ“³ö![]() µÄ×ų±źŗĶÅ×ĪļĻß
µÄ×ų±źŗĶÅ×ĪļĻß![]() µÄ½āĪöŹ½£»
µÄ½āĪöŹ½£»
£Ø2£©Å×ĪļĻß![]() ÉĻŹĒ·ń“ęŌŚµć
ÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() ŹĒÖ±½ĒČż½ĒŠĪ£æČē¹ū“ęŌŚ£¬ĒėĒó³öµćEµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
ŹĒÖ±½ĒČż½ĒŠĪ£æČē¹ū“ęŌŚ£¬ĒėĒó³öµćEµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©ČēĶ¼2£¬µć![]() ŌŚÅ×ĪļĻß
ŌŚÅ×ĪļĻß![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ·Ö±šŹĒÅ×ĪļĻß
·Ö±šŹĒÅ×ĪļĻß![]() £¬
£¬![]() ÉĻµÄ¶Æµć£¬ĒŅµć
ÉĻµÄ¶Æµć£¬ĒŅµć![]() µÄŗį×ų±źĻąĶ¬£¬¼Ē
µÄŗį×ų±źĻąĶ¬£¬¼Ē![]() Ć껿ĪŖ
Ć껿ĪŖ![]() £Øµ±µć
£Øµ±µć![]() Óėµć
Óėµć![]() ÖŲŗĻŹ±
ÖŲŗĻŹ±![]() £©£¬
£©£¬![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £Øµ±µć
£Øµ±µć![]() Óėµć
Óėµć![]() ÖŲŗĻŹ±£¬
ÖŲŗĻŹ±£¬![]() £©£¬Įī
£©£¬Įī![]() £¬¹Ū²ģĶ¼Ļ󣬵±
£¬¹Ū²ģĶ¼Ļ󣬵±![]() Ź±£¬Š“³ö
Ź±£¬Š“³ö![]() µÄȔֵ·¶Ī§£¬²¢Ēó³öŌŚ“Ė·¶Ī§ÄŚ
µÄȔֵ·¶Ī§£¬²¢Ēó³öŌŚ“Ė·¶Ī§ÄŚ![]() µÄ×ī“óÖµ£®
µÄ×ī“óÖµ£®

”¾“š°ø”æ£Ø1£©![]() £¬
£¬![]() £¬
£¬![]() £»£Ø2£©
£»£Ø2£©![]() »ņ
»ņ![]() £»ĄķÓɼū½āĪö£»£Ø3£©-2”Üx”Ü2£¬µ±
£»ĄķÓɼū½āĪö£»£Ø3£©-2”Üx”Ü2£¬µ±![]() Ź±£¬
Ź±£¬![]() µÄ×ī“óÖµĪŖ16£®
µÄ×ī“óÖµĪŖ16£®
”¾½āĪö”æ
£Ø1£©ÓÉÅ×ĪļĻß![]() £ŗ
£ŗ![]() æɵĆ
æɵĆ![]() £¬½«
£¬½«![]() £¬
£¬![]() “śČė
“śČė![]() £¬ĒóµĆ
£¬ĒóµĆ![]() £¬
£¬![]() £»
£»
£Ø2£©Ņ×µĆÖ±Ļß![]() µÄ½āĪöŹ½£ŗ
µÄ½āĪöŹ½£ŗ![]() £¬¢ŁČō
£¬¢ŁČō![]() ĪŖÖ±½Ē¶„µć£¬
ĪŖÖ±½Ē¶„µć£¬![]() £¬
£¬![]() £»¢ŚČō
£»¢ŚČō![]() ĪŖÖ±½Ē¶„µć£¬
ĪŖÖ±½Ē¶„µć£¬![]() £¬
£¬![]() £»¢ŪČō
£»¢ŪČō![]() ĪŖÖ±½Ē¶„µć£¬Éč
ĪŖÖ±½Ē¶„µć£¬Éč![]() ²»·ūŗĻĢāŅā£»
²»·ūŗĻĢāŅā£»
£Ø3£©ÓÉ![]() £¬µĆ
£¬µĆ![]() £¬Éč
£¬Éč![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬Ņ×ĒóÖ±Ļß
£¬Ņ×ĒóÖ±Ļß![]() µÄ½āĪöŹ½£ŗ
µÄ½āĪöŹ½£ŗ![]() £¬¹ż
£¬¹ż![]() ×÷
×÷![]() ÖįµÄĘ½ŠŠĻß
ÖįµÄĘ½ŠŠĻß![]() ½»
½»![]() ÓŚ
ÓŚ![]() £¬
£¬![]() £¬Éč
£¬Éč![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬Ņ×ÖŖ
£¬Ņ×ÖŖ![]() £¬
£¬![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £¬µ±
£¬µ±![]() Ź±£¬
Ź±£¬![]() µÄ×ī“óÖµĪŖ
µÄ×ī“óÖµĪŖ![]() .
.
£Ø1£©ÓÉÅ×ĪļĻß![]() £ŗ
£ŗ![]() æɵĆ
æɵĆ![]() £¬
£¬
½«![]() “śČė
“śČė![]()
µĆ![]() £¬
£¬
½āµĆ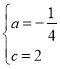 £¬
£¬
”ą![]() £¬
£¬
”ą![]() £»
£»
£Ø2£©Ņ×µĆÖ±Ļß![]() µÄ½āĪöŹ½£ŗ
µÄ½āĪöŹ½£ŗ![]() £¬
£¬
¢ŁČō![]() ĪŖÖ±½Ē¶„µć£¬
ĪŖÖ±½Ē¶„µć£¬![]() £¬
£¬
”ą![]() £¬
£¬
Ö±Ļß![]() ½āĪöŹ½ĪŖ
½āĪöŹ½ĪŖ![]()
ĮŖĮ¢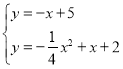 £¬
£¬
½āµĆ![]() »ņ
»ņ![]() £¬
£¬
”ą![]() £»
£»
¢ŚČō![]() ĪŖÖ±½Ē¶„µć£¬
ĪŖÖ±½Ē¶„µć£¬![]() £¬
£¬
Ķ¬ĄķµĆ![]() ½āĪöŹ½£ŗ
½āĪöŹ½£ŗ![]() £¬
£¬
ĮŖĮ¢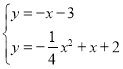 £¬
£¬
½āµĆ![]() »ņ
»ņ![]() £¬
£¬
”ą![]() £»
£»
¢ŪČō![]() ĪŖÖ±½Ē¶„µć£¬Éč
ĪŖÖ±½Ē¶„µć£¬Éč![]()
ÓÉ![]() µĆ
µĆ![]() £¬
£¬
¼“ £¬
£¬
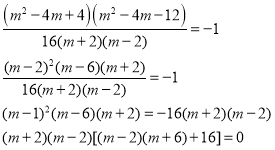
![]() »ņ
»ņ![]() £ØĪŽ½ā£©
£ØĪŽ½ā£©
½āµĆ![]() »ņ
»ņ![]() £Ø²»·ūŗĻĢāŅāÉįČ„£©£¬
£Ø²»·ūŗĻĢāŅāÉįČ„£©£¬
”ąµć![]() »ņ
»ņ![]() £»
£»
£Ø3£©”ß![]() £¬
£¬
”ą![]() £¬
£¬
Éč![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬
£¬
Ņ×ĒóÖ±Ļß![]() µÄ½āĪöŹ½£ŗ
µÄ½āĪöŹ½£ŗ![]() £¬
£¬
¹ż![]() ×÷
×÷![]() ÖįµÄĘ½ŠŠĻß
ÖįµÄĘ½ŠŠĻß![]() ½»
½»![]() ÓŚ
ÓŚ![]() £¬
£¬
Ōņ![]() £¬
£¬
![]()
![]()
Éč![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬Ņ×ÖŖ
£¬Ņ×ÖŖ![]() £¬
£¬
![]()
![]()
![]() £¬
£¬
µ±![]() Ź±£¬
Ź±£¬![]() µÄ×ī“óÖµĪŖ16£®
µÄ×ī“óÖµĪŖ16£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĪŖŅ»ĒŶ“µÄŠĪד£¬ĘäÕżŹÓĶ¼ŹĒÓÉŌ²»”![]() ŗĶ¾ŲŠĪABCD¹¹³É£®OµćĪŖ
ŗĶ¾ŲŠĪABCD¹¹³É£®OµćĪŖ![]() ĖłŌŚ”ŃOµÄŌ²ŠÄ£¬µćOÓÖĒ”ŗĆŌŚABĪŖĖ®Ćꓦ£®ČōĒŶ“æē¶ČCDĪŖ8Ć×£¬¹°øߣØOE”ĶĻŅCDÓŚµćF£©EFĪŖ2Ć×£®
ĖłŌŚ”ŃOµÄŌ²ŠÄ£¬µćOÓÖĒ”ŗĆŌŚABĪŖĖ®Ćꓦ£®ČōĒŶ“æē¶ČCDĪŖ8Ć×£¬¹°øߣØOE”ĶĻŅCDÓŚµćF£©EFĪŖ2Ć×£®
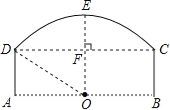
£Ø1£©Ēó![]() ĖłŌŚ”ŃOµÄ°ė¾¶DO£»
ĖłŌŚ”ŃOµÄ°ė¾¶DO£»
£Ø2£©ČōŗÓĄļŠŠŹ»Ą“Ņ»ĖŅÕżŹÓĶ¼ĪŖ¾ŲŠĪµÄ“¬£¬Ęäæķ6Ć×£¬Ā¶³öĖ®ĆęABµÄø߶ČĪŖhĆ×£¬Ēó“¬ÄÜĶعżĒŶ“Ź±µÄ×ī“óø߶Čh£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涬ĢģĄ“ĮĖ£¬É¹ŅĀ·ž³ÉĮĖĶ·ĢŪµÄŹĀĒ飬“ĻĆ÷µÄŠ”»ŖĻėµ½Ņ»øöŗĆ°ģ·Ø£¬ŌŚ¼ŅŗóŌŗµŲĆę£ØBD£©ÉĻĮ¢Į½øłµČ³¤µÄĮ¢ÖłAB”¢CD£Ø¾łÓėµŲĆę“¹Ö±£©£¬²¢ŌŚĮ¢ÖłÖ®¼äŠü¹ŅŅ»øłÉž×Ó£®ÓÉÓŚ¹ŅµÄŅĀ·ž±Č½Ļ¶ą£¬Éž×ӵĊĪד½üĖĘ³ÉĮĖÅ×ĪļĻßy=ax2-0.8x+c£¬ČēĶ¼1£¬ŅŃÖŖĮ¢ÖłAB=CD=2.6Ć×£¬BD=8Ć×£®
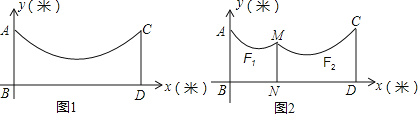
£Ø1£©ĒóÉž×Ó×īµĶµćĄėµŲĆęµÄ¾ąĄė£»
£Ø2£©ĪŖĮĖ·ĄÖ¹ŅĀ·žÅöµ½µŲĆę£¬Š”»ŖŌŚĄėABĪŖ3Ć×µÄĪ»ÖĆ“¦ÓĆŅ»øł“¹Ö±ÓŚµŲĆęµÄĮ¢ÖłMN³Åʚɞ×Ó£ØČēĶ¼2£©£¬Ź¹×ó±ßÅ×ĪļĻßF1µÄ×īµĶµć¾ąMNĪŖ1Ć×£¬ĄėµŲĆę1.6Ć×£¬ĒóMNµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĮ¬½Ó×ÅŗŗæŚ¼Æ¼Ņ¾×µÄ½ŗŗČżĒÅ£ØĒē“ØĒÅ£©£¬ŹĒŅ»×łĻĀ³ŠŹ½øֹܻģÄżĶĮĻµøĖ¹°ĒÅ£®ĖüÓĢČēŅ»µĄĆĄĄöµÄ²ŹŗēæēŌ½ŗŗ½£¬ŹĒ½³ĒĪäŗŗµÄŅ»µĄö¦Ąö¾°¹Ū£®ĒŵĹ°ĄßACBŹÓĪŖÅ×ĪļĻßµÄŅ»²æ·Ö£¬ĒÅĆę£ØŹÓĪŖĖ®Ę½µÄ£©Óė¹°ĄßÓĆ“¹Ö±ÓŚĒÅĆęµÄĻµøĖĮ¬½Ó£¬ĻąĮŚĻµøĖÖ®¼äµÄ¼ä¾ą¾łĪŖ5Ćףز»æ¼ĀĒĻµøĖµÄ“ÖĻø£©£¬¹°ĄßµÄæē¶ČABĪŖ280Ć×£¬¾ąĄė¹°ĄßµÄÓŅ¶Ė70Ćד¦µÄĻµøĖEFµÄ³¤¶ČĪŖ42Ć×£®ŅŌABĖłŌŚÖ±ĻßĪŖxÖį£¬Å×ĪļĻߵĶŌ³ĘÖįĪŖyÖį½ØĮ¢ČēĶ¼¢ŚĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµ£®
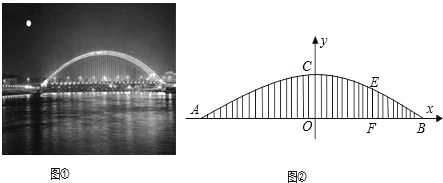
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ÕżÖŠ¼äĻµøĖOCµÄ³¤¶ČŹĒ¶ąÉŁĆ×£æŹĒ·ń“ęŌŚŅ»øłĻµøĖµÄ³¤¶ČĒ”ŗĆŹĒOC³¤¶ČµÄŅ»°ė£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
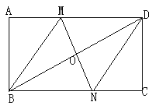
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬¶Ō½ĒĻßBDµÄ“¹Ö±Ę½·ÖĻßMNÓėADĻą½»ÓŚµćN£¬Į¬½ÓBM£¬DN.
£Ø1£©ĒóÖ¤£ŗĖıߊĪBMDNŹĒĮāŠĪ£»
£Ø2£©ČōAB=4£¬AD=8£¬ĒóMDµÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
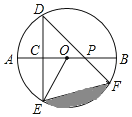
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬ĻŅDE“¹Ö±Ę½·Ö°ė¾¶OA£¬CĪŖ“¹×ć£¬ĻŅDFÓė°ė¾¶OBĻą½»ÓŚµćP£¬Į¬½ÓEF”¢EO£¬ČōDE£½2£¬”ĻDPA£½45”ć£®
£Ø1£©Ēó”ŃOµÄ°ė¾¶£»
£Ø2£©ĒóĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”ŃOŹĒ”÷ABCµÄĶā½ÓŌ²£¬”ĻABC=45”ć£¬OC”ĪAD£¬AD½»BCµÄŃÓ³¤ĻßÓŚD£¬AB½»OCÓŚE£®

£Ø1£©ĒóÖ¤£ŗADŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ŃOµÄÖ±¾¶ĪŖ6£¬Ļ߶ĪBC=2£¬Ēó”ĻBACµÄÕżĻŅÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(±¾ĢāĀś·Ö10·Ö)ŌĶĮĻĀĮŠ²ÄĮĻ£ŗ
£Ø1£©¹ŲÓŚxµÄ·½³Ģx2-3x+1=0£Øx”Ł0£©·½³ĢĮ½±ßĶ¬Ź±³ĖŅŌ![]() µĆ£ŗ
µĆ£ŗ ![]() ¼“
¼“![]() £¬
£¬ ![]() £¬
£¬
£Ø2£©a3+b3=£Øa+b£©£Øa2-ab+b2£©£»a3-b3=£Øa-b£©£Øa2+ab+b2£©£®
øł¾ŻŅŌÉĻ²ÄĮĻ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©x2-4x+1=0£Øx”Ł0£©£¬Ōņ![]() = ______ £¬
= ______ £¬ ![]() = ______ £¬
= ______ £¬ ![]() = ______ £»
= ______ £»
£Ø2£©2x2-7x+2=0£Øx”Ł0£©£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¶ž“ĪŗÆŹży£½x2+bx+cµÄĶ¼ĻóÓėxÖį½»ÓŚµćA£Ø1£¬0£©”¢B£Ø3£¬0£©£¬ÓėyÖį½»ÓŚµćC£®

£Ø1£©Ē󶞓ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ČōµćPĪŖÅ×ĪļĻßÉĻµÄŅ»µć£¬µćFĪŖ¶Ō³ĘÖįÉĻµÄŅ»µć£¬ĒŅŅŌµćA”¢B”¢P”¢FĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪ£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©µćEŹĒ¶ž“ĪŗÆŹżµŚĖÄĻóĻŽĶ¼ĻóÉĻŅ»µć£¬¹żµćE×÷xÖįµÄ“¹Ļߣ¬½»Ö±ĻßBCÓŚµćD£¬ĒóĖıߊĪAEBDĆ껿µÄ×ī“óÖµ¼°“ĖŹ±µćEµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com