
【题目】已知:![]() 为直线
为直线 ![]() 上的一点,以
上的一点,以![]() 为观察中心,射线
为观察中心,射线![]() 表示正北方向,
表示正北方向,![]() 表示正东方向(即
表示正东方向(即![]() ),射线
),射线![]() ,射线
,射线![]() 的方向如各图所示.
的方向如各图所示.
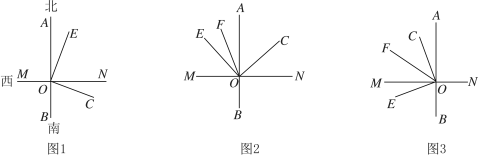
(1)如图1所示,当 ![]() 时:
时:
①若![]() ,则射线
,则射线![]() 的方向是 .
的方向是 .
② ![]() 与
与![]() 的关系为 ,
的关系为 ,
③ ![]() 与
与![]() 的关系为 .
的关系为 .
(2)若将射线![]() ,射线
,射线![]() 绕点
绕点![]() 旋转至图
旋转至图![]() 的位置,另一条射线
的位置,另一条射线![]() 恰好平分
恰好平分![]() ,旋转中始终保持
,旋转中始终保持![]() .
.
①若![]() ,则
,则![]() 度 .
度 .
②若![]() ,则
,则![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
(3)若将射线![]() ,射线
,射线![]() 绕点
绕点![]() 旋转至图
旋转至图![]() 的位置,射线
的位置,射线![]() 仍然平分
仍然平分![]() ,旋转中始终保持
,旋转中始终保持![]() ,则
,则![]() 与
与![]() 之间存在怎样的数量关系,并说明理由.
之间存在怎样的数量关系,并说明理由.
【答案】(1)①北偏东20°;②相等;③互补.(2)①24°;②2β.(3)∠CON=2∠AOF,理由见解析.
【解析】
(1)①根据方向角的定义即可求解;②根据同角的余角相等即可得出结论;③先根据同角的余角相等得出∠EON=∠BOC,再根据两角互补的定义即可得出结果.
(2)①根据同角的余角可知∠AOC=∠MOE,又根据角平分线的定义可得∠COF=∠MOF,两式相减即可得出结果.②由①知∠AOF=∠EOF=β,又由∠CON=∠AOE即可得出结果.
(3)根据角的和差,以及角平分线的定义即可求解.
解:(1)①北偏东20°
②∵由题意知,∠AOE+∠EON=90°,∠NOC+∠EON=90°,
∴∠AOE=∠CON.
③由题意知,∠BOC+∠NOC=90°,∠NOC+∠EON=90°,
∴∠BOC=∠EON,
又∠AOC+∠BOC=180°,
∴∠AOC+∠EON=180°.
故答案为:①北偏东20°;②相等;③互补.
(2)①由题意知,∠AOC+∠AOE=90°,∠MOE+∠AOE=90°,
∴∠AOC=∠MOE,
又OF为∠COM的角平分线,
∴∠COF=∠MOF,
∴∠COF-∠AOC =∠MOF-∠MOE,
∴∠AOF=∠EOF=24°.
②由①知,∠AOF=∠EOF=β,
∴∠CON=∠AOE=2∠AOF=2β.
故答案为:①24°;②2β.
(3)∵∠CON=180°-∠COM=180°-2∠MOF.
又∠AOF=90°-∠MOF,∴2∠AOF=180°-2∠MOF.
∴∠CON=2∠AOF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】发现来源于探究。小亮进行数学探究活动,作边长为a的正方形ABCD和边长边b的正方形AEFG(a>b),开始时点E在AB上,如图1,将正方形AEFG绕点A逆时针方向旋转。
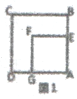
(1)如图2,小亮将正方形AEFG绕点A顺时针方向旋转,连接BE、DG,请证明:△ADG≌△ABE;
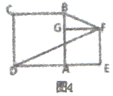
(2)如图3,小亮将正方形AEFG绕点A顺时针方向旋转,连接BE、DG,当点G恰好落在线段BE上,且a=3,b=2时,请你帮他求此时DG的长。
(3)如图4,小亮旋转正方形AEFG,当点E在DA的延长线上时,连接BF、DF,若FG平分∠BFD,请你帮他求a:b的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
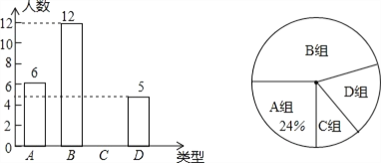
【题目】为了解学生课余活动情况,某班对参加A组:绘画;B组:书法;C组:舞蹈;D组:乐器;这四个课外兴趣小组的人员分布情况进行抽样调查,并根据收集的数据绘制了如图两幅不完整的统计图,请根据图中提供信息,解答下面的问题:
(1)此次共调查了多少名同学?
(2)将条形统计图补充完整,
(3)计算扇形统计图中书法部分的圆心角的度数;
(4)已知在此次调查中,参加D组的5名学生中有3名女生和2名男生,要从这5名学生中随机抽取2名学生参加市举办的音乐赛,用列表法或画树状图的方法求出抽取的2名学生恰好是1男1女的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
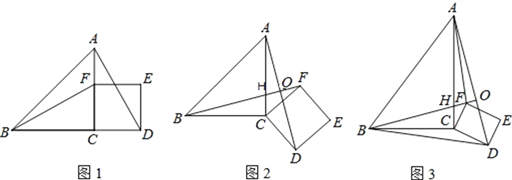
【题目】如图1,△ABC为等腰直角三角形,∠ACB=90,F是AC边上的一个动点(点F与A. C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度α,得到如图2的情形。图2中BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,并证明你的判断。
(3)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90,正方形CDEF改为矩形CDEF,如图3,且AC=4,BC=3,CD=![]() ,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
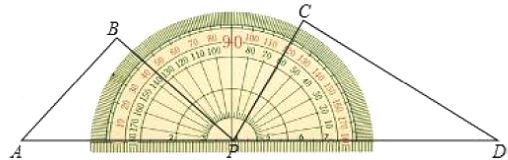
【题目】一副三角尺(分别含45°,45°,90°和30°,60°,90°)按如图所示摆放在量角器上,边PD与量角器0°刻度线重合,边AP与量角器180°刻度线重合,将三角尺ABP绕量角器中心点P以每秒10°的速度顺时针旋转,当边PB与0°刻度线重合时停止运动,设三角尺ABP的运动时间为t.
(1)当t=5时,边PB经过的量角器刻度线对应的度数是 度:
(2)若在三角尺ABP开始旋转的同时,三角尺PCD也绕点P以每秒2°的速度逆时针旋转,当三角尺ABP停止旋转时,三角尺PCD也停止旋转.
①当t为何值时,边PB平分∠CPD;
②在旋转过程中,是否存在某一时刻使∠BPD=2∠APC,若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)读读做做:平行线是平面几何中最基本、也是非常重要的图形.在解决某些平面几何问题时,若能依据问题的需要,添加恰当的平行线,往往能使证明顺畅、简洁.请根据上述思想解决教材中的问题:如图①,AB∥CD,则∠B+∠D ∠E(用“>”、“=”或“<”填空);
(2)倒过来想:写出(1)中命题的逆命题,判断逆命题的真假并说明理由.
(3)灵活应用:如图②,已知AB∥CD,在∠ACD的平分线上取两个点M、N,使得∠AMN=∠ANM,求证:∠CAM=∠BAN.
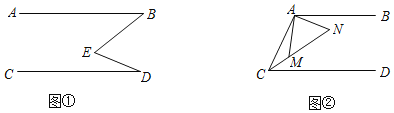
查看答案和解析>>
科目:初中数学 来源: 题型:
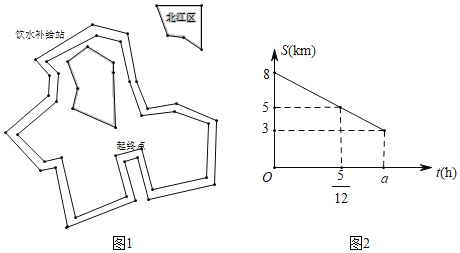
【题目】“2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行,小林参加了环绕湖8km的迷你马拉松项目(如图1),上午8:00起跑,赛道上距离起点5km处会设置饮水补给站,在比赛中,小林匀速前行,他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示
(1)求小林从起点跑向饮水补给站的过程中与t的函数表达式
(2)求小林跑步的速度,以及图2中a的值
(3)当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午8:55之前跑到终点,那么接下来一段路程他的速度至少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了了解学生在数学学习中的纠错情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的八年级(5)班和八年级(6)班进行了检测.并从两班各随机抽取10名学生的得分绘制成下列两个统计图.根据以上信息,整理分析数据如下:
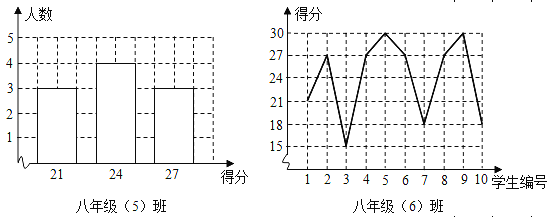
班级 | 平均分(分) | 中位数(分) | 众数(分) |
八年级(5)班 | a | 24 | 24 |
八年级(6)班 | 24 | b | c |
(1)求出表格中a,b,c的值;
(2)你认为哪个班的学生纠错得分情况比较整齐一些,通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
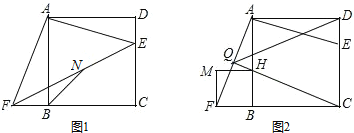
【题目】如图1,点E是正方形ABCD的边CD上一点(不与C、D重合),连接AE,过点A作AF⊥AE交CB的延长线于点F
(1)求证:AE=AF;
(2)连接EF,N为EF之中点,连接BN,求![]() 的值;
的值;
(3)以BF为边作正方形BFMH,如图2,CH与AF相交于点Q,当E在CD上运动(不与C、D重合),问∠CQD的大小是否发生变化?若不变,求其值;若变化,请指出其范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com