
【题目】若矩形的一个短边与长边的比值为![]() ,(黄金分割数),我们把这样的矩形叫做黄金矩形
,(黄金分割数),我们把这样的矩形叫做黄金矩形
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD.
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由.
(3)归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)

【答案】(1)见解析;(2)矩形EBCF不是黄金矩形,理由见解析;(3)若以黄金矩形的短边为边在矩形内作(截割)正方形,则剩余矩形必为黄金矩形.
【解析】
(1)如图,分两种情况:正方形中,AD的对边在矩形的内部或外部;
(2)矩形EBCF不是黄金矩形, 设AB=a,AD=b(a>b),则BE=BA+AE=a+b,BE′=BA-E′A=a-b,由已知得![]() =
=![]() ,所以
,所以![]() =
=![]() =
=![]() ÷(1+
÷(1+![]() )=
)=![]() ÷(1+
÷(1+![]() )=
)=![]() ≠
≠![]() ,对应边不成比例,故矩形EBCF不是黄金矩形;矩形E′BCF′是黄金矩形,
,对应边不成比例,故矩形EBCF不是黄金矩形;矩形E′BCF′是黄金矩形,
理由:![]() =
=![]() =(1-
=(1-![]() )÷
)÷![]() =(1-
=(1-![]() )÷
)÷![]() =
=![]() ,即对应边成比例,故两个矩形相似.
,即对应边成比例,故两个矩形相似.
(3)由(1)、(2)可发现结论:若以黄金矩形的短边为边在矩形内作(截割)正方形,则剩余矩形必为黄金矩形.
解:(1)以AD为边可作出两个正方形AEFD与AE′F′D′(AB>AD),如图所示

(2)矩形EBCF不是黄金矩形,理由如下:
设AB=a,AD=b(a>b),则BE=BA+AE=a+b,BE′=BA-E′A=a-b,
由ABCD为黄金矩形,得![]() =
=![]()
∴![]() =
=![]() =
=![]() ÷(1+
÷(1+![]() )=
)=![]() ÷(1+
÷(1+![]() )=
)=![]() ≠
≠![]()
∴矩形EBCF不是黄金矩形;
矩形E′BCF′是黄金矩形.
证明:如图,∵![]() =
=![]() =(1-
=(1-![]() )÷
)÷![]() =(1-
=(1-![]() )÷
)÷![]() =
=![]()
∴E′BCF′是黄金矩形
(3)由(1)、(2)可发现结论:若以黄金矩形的短边为边在矩形内作(截割)正方形,则剩余矩形必为黄金矩形.


科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =![]() ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作![]() ,使AE=AD,
,使AE=AD,![]() +
+![]() =180°.
=180°.
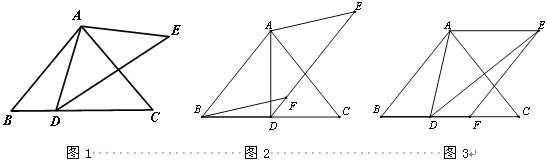
(1)直接写出∠ADE的度数(用含![]() 的式子表示);
的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
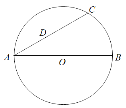
【题目】如图,线段AB是⊙O的直径,点C在⊙O上,且∠CAB=30°,设点D是线段AC上任意一点(不含端点),连接OD,当![]() CD+OD的最小值为9时,则⊙O的直径AB的长为_____.
CD+OD的最小值为9时,则⊙O的直径AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图,
①利用刻度尺在∠AOB的两边OA,OB上分别取OM=ON;
②利用两个三角板,分别过点M,N画OM,ON的垂线,交点为P;
③画射线OP.则射线OP为∠AOB的平分线.

(1)请写出射线OP为∠AOB的平分线的证明过程.
(2)请根据你的证明过程,写出小林的画法的依据______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有不重合的两个点Q(x1,y1)与P(x2,y2).若Q,P为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x轴或y轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“折距”,记做DPQ.特别地,当PQ与某条坐标轴平行(或重合)时,线段PQ的长即点Q与点P之间的“折距”.例如,在图1中,点P(1,-1),点Q(3,-2),此时点Q与点P之间的“折距”DPQ=3.
(1)①已知O为坐标原点,点A(3,-2),B(-1,0),则DAO=______,DBO=______.
②点C在直线y=-x+4上,请你求出DCO的最小值.
(2)点E是以原点O为圆心,1为半径的圆上的一个动点,点F是直线y=3x+6上以动点.请你直接写出点E与点F之间“折距”DEF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
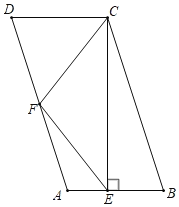
【题目】如图,在四边形ABCD中,AD∥BC,AD=BC=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF.
(1)若∠ADC=80°,求∠ECF;
(2)求证:∠ECF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为1,点
的边长为1,点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的负半轴上将正方形
轴的负半轴上将正方形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至正方形
至正方形![]() 的位置,
的位置,![]() 与
与![]() 相交于点
相交于点![]() ,则
,则![]() 的坐标为____________.
的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A,B两点,与y轴交于C点,抛物线![]() 经过A,B,C三点,顶点为F.
经过A,B,C三点,顶点为F.
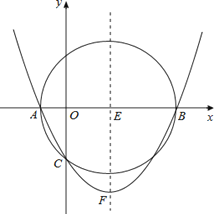
(1)求A,B,C三点的坐标;
(2)求抛物线的解析式及顶点F的坐标;
(3)已知M为抛物线上一动点(不与C点重合),试探究:
①使得以A,B,M为顶点的三角形面积与△ABC的面积相等,求所有符合条件的点M的坐标;
②若探究①中的M点位于第四象限,连接M点与抛物线顶点F,试判断直线MF与⊙E的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,点P在AB的延长线上,PC与⊙O相切于点C,点D为弧AC上的点,且2∠DAB﹣∠P=90°,连接AD.
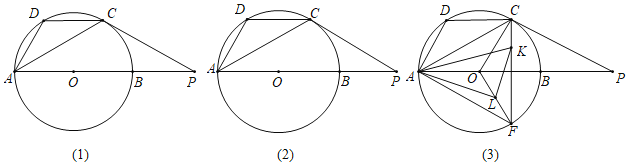
(1)如图1,求证:弧AD=弧BC;
(2)如图2,PC=6,PB=![]() ,求∠ADC度数;
,求∠ADC度数;
(3)如图3,在(2)的条件下,F为AB下方⊙O上一点.∠ACF=60°,L为OF中点,LK⊥AL于L,交CF于点K.连接AK,求AK的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com