
【题目】为了加强公民节水意识,合理利用水资源,某市采用价格调控手段达到节约用水的目的,规定:每户居民每月用水不超过15m3时,按基本价格收费;超过15m3时,不超过的部分仍按基本价格收费,超过的部分要加价收费,该市某户居民今年4、5月份的用水量和水费如表所示:
月份 | 用水量/m3 | 水费/元 |
4 | 16 | 50 |
5 | 20 | 70 |
(1)求该市居民用水的两种收费价格;
(2)若该居民6月份交水费80元,那么该居民这个月水量为m3 .
 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.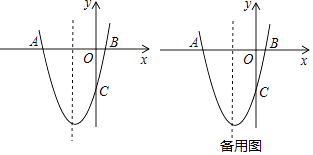
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自4月以来,我市推出了一项“共享单车”的便民举措,为人们的城市生活出行带来了方便.图(1)所示的是某款单车的实物图.图(2)是这辆单车的部分几何示意图,其中车支架BC的长为20cm,且∠CBA=75°,∠CAB=30°.求车架档AB的长.(参考数据:sin75°= ![]() ,cos75°=
,cos75°= ![]() ,tan75°=2+
,tan75°=2+ ![]() )
)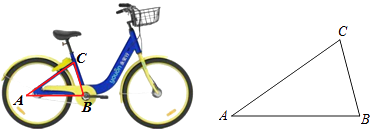
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“单词的记忆效率“是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.如图描述了某次单词复习中小华,小红小刚和小强四位同学的单词记忆效率y与复习的单词个数x的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )

A. 小华B. 小红C. 小刚D. 小强
查看答案和解析>>
科目:初中数学 来源: 题型:
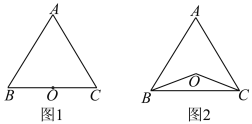
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证:∠ABC=∠ACB;
(2)如图2,若点O在△ABC的内部,则∠ABC=∠ACB成立吗?并说明理由;
(3)若点O在△ABC的外部,则∠ABC=∠ACB成立吗?请画图表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)210+29+28+…+2+1
(2)3n+3n-1+3n-2…+3+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的![]() ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com