练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
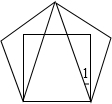
    15．将边长相等的一个正方形与一个正五边形，按如图重叠放置，则∠1度数=18°．

    分析 利用多边形内角和公式求得∠E的度数，在等腰三角形AED中可求得∠EAD的度数，进而求得∠BAD的度数，再利用正方形的内角得出∠BAG=90°，进而得出∠DAG的度数．

    解答 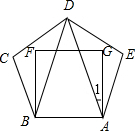解：∵正五边形ABCDE的内角和为（5-2）×180°=540°，
    ∴∠E=$\frac{1}{5}$×540°=108°，∠BAE=108°
    又∵EA=ED，
    ∴∠EAD=$\frac{1}{2}$×（180°-108°）=36°，
    ∴∠BAD=∠BAE-∠EAD=72°，
    ∵正方形GABF的内角∠BAG=90°，
    ∴∠1=90°-72°=18°，
    故答案为：18°．

    点评 本题考查了正多边形的计算，重点掌握正多边形内角和公式是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）[（2a-b）2-（2a+b）（2a-b）-6b]÷（2b）
    （2）运用整式乘法公式进行计算：3.142+6.28×0.86+0.862．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，三个小正方形的边长都为3，则图中阴影部分面积的和是$\frac{27}{8}$π．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，在△ABC中，AB=AC，它的内切圆分别切AB，AC于点E，F，若AB=100，BC=60，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．一元二次方程x2+8x-9=0配方后得到的方程是（　　）
    A．（x-4）2+7=0B．（x+4）2=25C．（x-4）2=25D．（x+4）2-7=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．请从以下两个小题中任选一个作答，若多选，按选做的第一题计分．
    A：如图1，AD是正五边形ABCDE的一条对角线，则∠BAD=72°．
    B：如图2，小明从坡角为27.5°的斜坡的坡底A走到离A水平距离10米远（AC=10米）的B处，则他走过的坡面距离AB为11.27米（结果精确到0.01米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．己知代数式-2x+4
    （1）-2x+4是x的函数（填“是”或≤“不是”）；
    （2）当x取3-a时，请你以a的取值为横坐标，对应的-2x+4的值为纵坐标，画出其图象；
    （3）若（2）中的图象与横轴、纵轴分别相交于点A、B，点P在线段AB上（不与A，B重合），P到横轴、纵轴的距离分别为d1、d2，求d1，d2的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列各数中，-3的倒数是（　　）
    A．3B．$-\frac{1}{3}$C．$\frac{1}{3}$D．-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

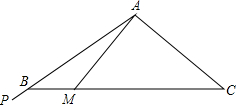    13．在等腰△ABC中AB=AC，∠BAC=120°，在边AB的延长线上有一点P，射线AP从AB开始，绕点A逆时针匀速旋转，每秒钟旋转15°，到达AC后立即以相同旋转速度返回AB，到达后立即重复上述旋转过程．当AP旋转1秒时，此时光线AP交BC于点M，BM的长为（20$\sqrt{3}$-20）cm，光线AP从AB处旋转开始计时，若要转2018秒，射线AP与BC边的交点与点B之间的距离是（20$\sqrt{3}$-10）cm．

    查看答案和解析>>

    同步练习册答案