
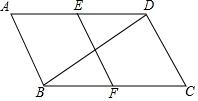
 如图,在?ABCD中,∠C=60°,E,F分别是AD,BC的中点,BC=2CD=4.
如图,在?ABCD中,∠C=60°,E,F分别是AD,BC的中点,BC=2CD=4.分析 (1)由平行四边形的性质得出AD∥BC,AD=BC,证出DE∥CF,DE=CF,得出四边形CDEF是平行四边形,证出CD=CF,即可得出四边形CDEF是菱形;
(2)连接DF,证明△CDF是等边三角形,得出∠CDF=∠CFD=60°,求出∠BDF=30°,证出∠BDC=∠BDF+∠CDF=90°,由勾股定理即可得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵E,F分别是AD,BC的中点,
∴DE=$\frac{1}{2}$AD,CF=$\frac{1}{2}$BC,
∴DE∥CF,DE=CF,
∴四边形CDEF是平行四边形,
又∵BC=2CD,
∴CD=CF,
∴四边形CDEF是菱形;
(2)解:连接DF,如图所示:
∵CD=CF,∠C=60°,
∴△CDF是等边三角形,
∴∠CDF=∠CFD=60°,
∵BF=DF,
∴∠BDF=30°,
∴∠BDC=∠BDF+∠CDF=90°,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 本题考查的是菱形的判定与性质、平行四边形的判定和性质、等边三角形的判定与性质、勾股定理等知识;熟练掌握平行四边形的判定与性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标可以为( )
如图,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标可以为( )| A. | (3,-2) | B. | (4,0) | C. | (5,-1) | D. | (5,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
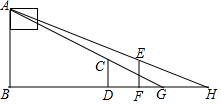 雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.
雯雯和笑笑想利用皮尺和所学的几何知识测量学校操场上旗杆的高度,他们的测量方案如下:当雯雯站在旗杆正前方地面上的点D处时,笑笑在地面上找到一点G,使得点G、雯雯的头顶C以及旗杆的顶部A三点在同一直线上,并测得DG=2.8m;然后雯雯向前移动1.5m到达点F处,笑笑同样在地面上找到一点H,使得点H、雯雯的头顶E以及旗杆的顶部A三点在同一直线上,并测得GH=1.7m,已知图中的所有点均在同一平面内,AB⊥BH,CD⊥BH,EF⊥BH,雯雯的身高CD=EF=1.6m.请你根据以上测量数据,求该校旗杆的高度AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com