
| A. | ①②③ | B. | ①③⑤ | C. | ②④⑤ | D. | ③④⑤ |
分析 ①分x<-1,-1<x<0、0<x<1、x>1找出y的正负,由此可得出函数图象经过第一、二、三、四象限,①错误;②由x在分母上可得出x≠0,函数图象与y轴无交点,②正确(其实得出①不正确,②正确即可确定答案了);③由当x=±1时,y=x-$\frac{1}{x}$=0,可得出函数图象与x轴的交点坐标为(-1,0)、(1,0),③错误;④设点(m,n)(m≠0)为函数y=x-$\frac{1}{x}$图象上任意一点,根据函数图象上点的坐标特征可得出点(-m,-n)在函数y=x-$\frac{1}{x}$的图象上,即图象关于原点成中心对称,④正确;⑤利用做差法确定当x>0时,y随x的增大而增大,⑤正确.综上即可得出结论.
解答 解:①当x<-1时,y=x-$\frac{1}{x}$<0;
当-1<x<0时,y=x-$\frac{1}{x}$>0;
当0<x<1时,y=x-$\frac{1}{x}$<0;
当x>1时,y=x-$\frac{1}{x}$>0.
∴函数图象经过第一、二、三、四象限,①错误;
②∵x为分母,
∴x≠0,
∴函数图象与y轴无交点,②正确;
③当x=±1时,y=x-$\frac{1}{x}$=0,
∴函数图象与x轴的交点坐标为(-1,0)、(1,0),③错误;
④设点(m,n)(m≠0)为函数y=x-$\frac{1}{x}$图象上任意一点,
则n=m-$\frac{1}{m}$,-n=-m+$\frac{1}{m}$=-(m-$\frac{1}{m}$),
∴点(-m,-n)在函数y=x-$\frac{1}{x}$的图象上,
∴图象关于原点成中心对称,④正确;
⑤当x>0时,设0<x1<x2,
则y2-y1=x2-$\frac{1}{{x}_{2}}$-(x1-$\frac{1}{{x}_{1}}$)=(x2-x1)+($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$)=(x2-x1)+$\frac{{x}_{2}-{x}_{1}}{{x}_{1}•{x}_{2}}$=(x2-x1)(1+$\frac{1}{{x}_{1}•{x}_{2}}$)>0,
∴当x>0时,y随x的增大而增大,⑤正确.
综上所述:正确的结论有②④⑤.
故选C.
点评 本题考查了反比例函数的性质、一次函数的性质,逐一分析五条结论的正误是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
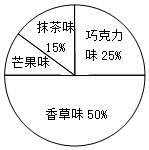 某冷饮店一天售出各种口味冰淇淋份数的扇形统计图如图所示.如果知道香草口味冰淇淋一天售出200份,那么芒果口味冰淇淋一天售出的份数是( )
某冷饮店一天售出各种口味冰淇淋份数的扇形统计图如图所示.如果知道香草口味冰淇淋一天售出200份,那么芒果口味冰淇淋一天售出的份数是( )| A. | 80 | B. | 40 | C. | 20 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com