
如图所示,点 是⊙
是⊙ 上一点,⊙
上一点,⊙ 与⊙
与⊙ 相交于
相交于 、
、 两点,
两点, ,垂足为
,垂足为 ,分别交⊙
,分别交⊙ 、⊙
、⊙ 于
于 、
、 两点,延长
两点,延长 交⊙
交⊙ 于
于 ,交
,交 的延长线于
的延长线于 ,
, 交
交 于
于 ,连结
,连结 .
.
【小题1】求证: ;
;
【小题2】若 ,求证:
,求证: ;
;
【小题3】 若 ,且线段
,且线段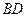 、
、 的长是关于
的长是关于 的方程
的方程 的两个实数根,求
的两个实数根,求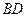 、
、 的长.
的长.
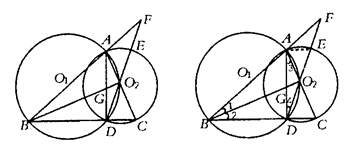
【小题1】∵BC⊥AD于D,
∴∠BDA=∠CDA=90°,
∴AB、AC分别为⊙O1、⊙O2的直径.
∵∠2=∠3,∠BGD+∠2=90°,∠C+∠3=90°,
∴∠BGD=∠C.
【小题2】∵∠DO2C=45°,∴∠ABD=45°
∵O2D=O2C,
∴∠C=∠O2DC=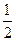 (180°-∠DO2C)=67.5°,
(180°-∠DO2C)=67.5°,
∴∠4=22.5°,·
∵∠O2DC=∠ABD+∠F,
∴∠F=∠4=22.5°,∴AD=AF.
【小题3】∵BF=6CD,∴设CD=k,则BF=6k.
连结AE,则AE⊥AD,∴AE∥BC,
∴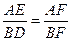 ∴AE·BF=BD·AF.
∴AE·BF=BD·AF.
又∵在△AO2E和△DO2C中,AO2=DO2
∠AO2E=∠DO2C, O2E=O2C,
∴△AO2E≌△DO2C,∴AE=CD=k,
∴6k2=BD·AF=(BC-CD)(BF-AB).
∵∠BO2A=90°,O2A=O2C,∴BC=AB.
∴6k2=(BC-k)(6k-BC).∴BC2-7kBC+12k2=0,
解得:BC=3k或BC=4k.
当BC=3k,BD=2k.
∵BD、BF的长是关于x的方程x2-(4m+2)x+4m2+8=0的两个实数根.
∴由根与系数的关系知:BD+BF=2k+6k=8k=4m+2.
整理,得:4m2-12m+29=0.
∵△=(-12)2-4×4×29=-320<0,此方程无实数根.
∴BC=3k(舍).
当BC=4k时,BD=3k.
∴3k+6k=4m+2,18k2=4m2+8,整理,
得:m2-8m+16=0,
解得:m1=m2=4,
∴原方程可化为x2-18x+72=0,
解得:x1=6,x2=12, ∴BD=6,BF=12.
解析


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
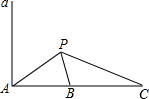 如图所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处,某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号,在当时气象条件下,声波在水中的传播速度是1.5 km/s.
如图所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处,某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号,在当时气象条件下,声波在水中的传播速度是1.5 km/s.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•江津区模拟)如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(2012•江津区模拟)如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处,某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号,在当时气象条件下,声波在水中的传播速度是1.5 km/s.
如图所示,a是海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处,某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号,在当时气象条件下,声波在水中的传播速度是1.5 km/s.查看答案和解析>>
科目:初中数学 来源:2008年江苏省扬州市高邮中学教改班招生考试数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2007年浙江省温州市乐清中学自主招生考试数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com