练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    解方程组．


    解：，①+②得：5x=10，即x=2，

    将x=2代入①得：y=1，则方程组的解为．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    某发电厂共有6台发电机发电，每台的发电量为300万千瓦/月．该厂计划从今年7

    月份开始到年底，对6台发电机各进行一次改造升级．每月改造升级1台，这台发电机当月停机，并

    于次月再投入发电，每台发电机改造升级后，每月的发电量将比原来提高20%．已知每台发电机改造

    升级的费用为20万元，将今年7月份作为第1个月开始往后算，该厂第x（x是正整数）个月的发电

    量设为y（万千瓦）．

    （1）求该厂第2个月的发电量及今年下半年的总发电量；

    （2）求y关于x的函数关系式；

    （3）如果每发1千瓦电可以盈利0.04元，那么从第1个月开始，至少要到第几个月，这期间该厂的

            发电盈利扣除发电机改造升级费用后的盈利总额w1（万元），将超过同样时间内发电机不作改造

            升级时的发电盈利总额w2（万元）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：﹣×=  ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知Rt△ABC中，∠C=90°，AC=4，tanA=，则BC的长是（　　）

    　   A．2                     B．                             8    C．                       2  D． 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：50°﹣15°30′=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


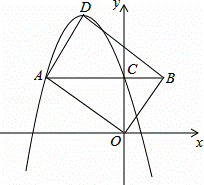
    如图，已知在平面直角坐标系xOy中，O是坐标原点，抛物线y=﹣x2+bx+c（c＞0）的顶点为D，与y轴的交点为C，过点C作CA∥x轴交抛物线于点A，在AC延长线上取点B，使BC=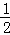AC，连接OA，OB，BD和AD．

    （1）若点A的坐标是（﹣4，4）

    ①求b，c的值；

    ②试判断四边形AOBD的形状，并说明理由；

    （2）是否存在这样的点A，使得四边形AOBD是矩形？若存在，请直接写出一个符合条件的点A的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知函数y=ax+b经过（1,3）（0，-2）求a-b（     ）

    A.-1    B.-3      C.3    D.7

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，-4），

    （1）求抛物线解析式；

    （2）将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，求当△BEF与△BAO相似时，E点坐标；

    （3）记平移后抛物线与AB另一个交点为G，则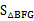与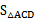是否存在8倍的关系，若有，写出F点坐标。

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，正方形ABCD边长为1，当M、N分别在BC，CD上，使得△CMN的周长为2，则△AMN的面积的最小值为           .

    　

    查看答案和解析>>

    同步练习册答案