
【题目】
(1)计算: ![]() ﹣4sin30°+(2014﹣π)0﹣22 .
﹣4sin30°+(2014﹣π)0﹣22 .
(2)解不等式组: ![]() .
.
【答案】
(1)解:原式=3﹣4× ![]() +1﹣4
+1﹣4
=3﹣2+1﹣4
=﹣2
(2)解:由①得:x>2;
由②得:x<3,
故不等式的解集为2<x<3
【解析】(1)原式第一项利用二次根式的定义化简,第二项利用特殊角的三角函数值计算,第三项利用零指数幂法则计算,最后一项利用乘方的意义化简,计算即可得到结果;(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
【考点精析】通过灵活运用零指数幂法则和一元一次不等式组的解法,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )即可以解答此题.


科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”
译文:“有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?设有x个人共同买鸡,根据题意列一元一次方程._____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果两个一元一次方程的解互为相反数,我们就称这两个方程为“兄弟方程”.
如方程2x=4和3x+6=0为“兄弟方程”.
(1)若关于x的方程5x+m=0与方程2x﹣4=x+1是“兄弟方程”,求m的值;
(2)若两个“兄弟方程”的两个解的差为8,其中一个解为n,求n的值;
(3)若关于x的方程2x+3m﹣2=0和3x﹣5m+4=0是“兄弟方程”,求这两个方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N。
(1)求证:MN=AM+BN;

(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 . 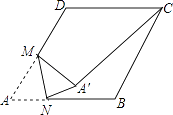
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=﹣ ![]() 的函数交于A(﹣2,b),B两点.
的函数交于A(﹣2,b),B两点. 
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a﹣b+c,则P的取值范围是( ) 
A.﹣4<P<0
B.﹣4<P<﹣2
C.﹣2<P<0
D.﹣1<P<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知MN∥PQ,点B在MN上,点C在PQ上,点A在点B的左侧,点D在点C的右侧,∠ADC,∠ABC的平分线相交于点E(不与B,D点重合),∠CBN=110°.
(1)若∠ADQ=140°,写出∠BED的度数 (直接写出结果即可);
(2)若∠ADQ=m°,将线段AD沿DC方向平移,使点D移动到点C的左侧,其他条件不变,如图②所示,求∠BED的度数(用含m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
为促进学生健康成长,切实提高学生健康水平,某校为各班用400元购进若干体育用品,接着又用450元购进第二批体育用品,已知第二批所购体育用品数是第一批所购体育用品数的1.5倍,且每件体育用品的进价比第一批的进价少5元,求第一批体育用品每件的进价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com