
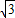 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1,O2分别从点A、点B同时出发,运动的时间为ts.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1,O2分别从点A、点B同时出发,运动的时间为ts.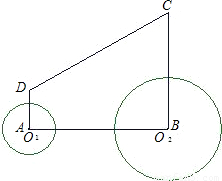
 解:(1)∵当⊙O2与腰CD相切时,EF的长为⊙O2的半径,
解:(1)∵当⊙O2与腰CD相切时,EF的长为⊙O2的半径,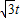 ,
,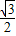 ;
; )秒;
)秒;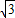 =6
=6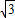 ,
,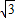 -
-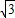 t,
t, -
- t)2=62,即t2-9t+18=0,
t)2=62,即t2-9t+18=0,

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
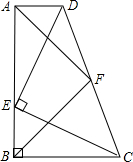 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.查看答案和解析>>
科目:初中数学 来源: 题型:
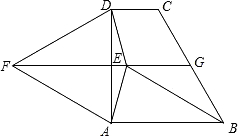 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.查看答案和解析>>
科目:初中数学 来源: 题型:
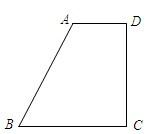 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.查看答案和解析>>
科目:初中数学 来源: 题型:
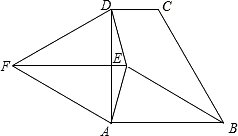 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com