已知：如图，在△ABC中，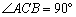
，D是BC的中点，
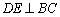，CE∥AD．如果AC=2，CE=4．
（1）求证：四边形ACED是平行四边形；
（2）求四边形ACEB的周长；
（3）直接写出CE和AD之间的距离．
（1）证明：∵∠ACB=90°，DE⊥BC，∴AC∥DE. ……………………………1分
又∵CE∥AD，
∴四边形ACED是平行四边形. ………2分
（2）解：∵四边形ACED的是平行四边形.
∴DE=AC=2.
在Rt△CDE中，∵∠CDE=90°，
由勾股定理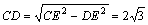
.……………………………………3分
∵D是BC的中点，
∴BC=2CD=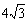
.
在Rt△ABC中，∵∠ACB=90°，
由勾股定理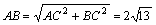
.…………………………………4分
∵D是BC的中点，DE⊥BC，
∴EB=EC=4.
∴四边形ACEB的周长= AC+CE+EB+BA=10+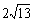
.…………………5分
（3）解：CE和AD之间的距离是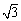
．……………………………………………6分
科目：初中数学 来源： 题型：
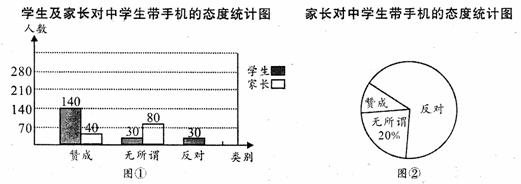
“校园手机”现象越来越受到社会的关注．“寒假”期间，某校小记者随机调查了某地区若干名学生和家长对学生带手机现象的看法，统计整理并制作了如下的统计图：
(1)求这次调查的家长人数，并补全图①；
(2)求图②中表示家长“赞成”的圆心角的度数；
(3)已知某地区共6500名家长，估计其中反对中学生带手机的家长大约有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系xOy中，直线x=2和直线y=ax交于点A，过A作AB⊥x轴于点B．如果a取1，2，3，…，n（n为正整数）时，对应的△AOB的面积为S1，S2，S3，…，Sn，那么S1= ；S1+S2+S3+…+Sn= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图1，在平面直角坐标系xOy中，等腰直角△AOB的斜边OB在x上，顶点A的坐标为（3，3）.
（1）求直线OA的解析式；
（2）如图2，如果点P是x轴正半轴上的一个动点，过点P作PC∥y轴，交直线OA于点C，设点P的坐标为（m，0），以A、C、P、B为顶点的四边形面积为S，求S与m之间的函数关系式；
（3）如图3，如果点D（2，a）在直线AB上. 过点O、D作直线OD，交直线PC于点E，在CE的右侧作矩形CGFE，其中CG=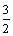
，请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.
图1 图2 图3
查看答案和解析>>
科目：初中数学 来源： 题型：
已知⊙O1、⊙O2的半径不相等，⊙O1的半径长为3，若⊙O2上的点A满足AO1＝3，
则⊙O1与⊙O2的位置关系是
A．相交或相切 B．相切或相离 C．相交或内含 D．相切或内含
查看答案和解析>>
科目：初中数学 来源： 题型：
刘翔为了迎战2008年北京奥运会刻苦进行110米拦训练，教练对他的10次训练成绩进行统计分析，若要判断他的成绩是否稳定，则教练需要知道刘翔这10次成绩的 （ ）A．平均数 B．中位数 C．众数 D．方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
初中毕业生总数将达到52500人，这个数据用科学计数法可表示为 ．