
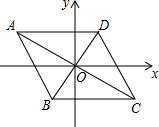
 如图,已知点A(-4,2),B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.
如图,已知点A(-4,2),B(-1,-2),平行四边形ABCD的对角线交于坐标原点O.分析 (1)利用中心对称图形的性质得出C,D两点坐标;
(2)利用平行四边形的性质以及结合平移的性质得出即可;
(3)利用SABCD的可以转化为边长为;5和4的矩形面积,进而求出即可.
解答 解:(1)∵四边形ABCD是平行四边形,
∴四边形ABCD关于O中心对称,
∵A(-4,2),B(-1,-2),
∴C(4,-2),D(1,2);
(2)线段AB到线段CD的变换过程是:绕点O旋转180°;
(3)由(1)得:A到y轴距离为:4,D到y轴距离为:1,
A到x轴距离为:2,B到x轴距离为:2,
∴SABCD的可以转化为边长为;5和4的矩形面积,
∴SABCD=5×4=20.
点评 此题主要考查了平行四边形的性质以及中心对称图形的性质,根据题意得出SABCD的可以转化为矩形面积是解题关键.


科目:初中数学 来源: 题型:填空题
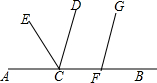 如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为90-$\frac{α}{2}$度(用关于α的代数式表示).
如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为90-$\frac{α}{2}$度(用关于α的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
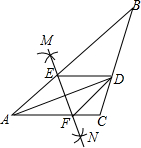 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
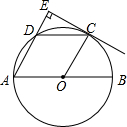 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
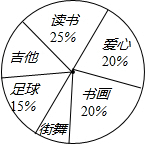 901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a3b-a2b=2 | |
| B. | 单项式-x2的系数是-1 | |
| C. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-1 | |
| D. | 若分式$\frac{{a}^{2}-1}{a+1}$的值等于0,则a=±1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
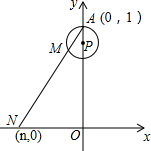 如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2x+3x=x | B. | 6xy2÷2xy=3y | C. | (-2x2y)3=-6x6y3 | D. | 2xy2•(-x)=-2x2y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com