
【题目】如图,在菱形![]() 中,
中,![]() ,点
,点![]() 分别是线段
分别是线段![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .给出如下几个结论:
.给出如下几个结论:
①![]()
②![]() 平分
平分![]() ;
;
③若![]() ,则
,则![]()
④![]()
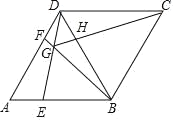
其中正确的结论是_____________(填写所有正确结论的序号).
【答案】①②④
【解析】
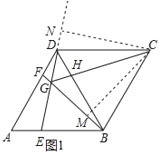
根据菱形的性质得到AB=AD,推出△ABD为等边三角形,得到∠A=∠BDF=60![]() ,根据全等三角形的判定得到△AED≌△DFB;过点C作CM⊥GB于M,CN⊥GD于N(如图1),根据全等三角形的性质得到CN=CM,根据角平分线的定义得到CG平分∠BGD;过点F作FP∥AE交DE于P点(如图2),根据平行线分线段成比例定理得到BG=6GF,再得到
,根据全等三角形的判定得到△AED≌△DFB;过点C作CM⊥GB于M,CN⊥GD于N(如图1),根据全等三角形的性质得到CN=CM,根据角平分线的定义得到CG平分∠BGD;过点F作FP∥AE交DE于P点(如图2),根据平行线分线段成比例定理得到BG=6GF,再得到![]() ;推出B、C、D、G四点共圆,根据圆周角定理得到∠BGC=∠BDC=60
;推出B、C、D、G四点共圆,根据圆周角定理得到∠BGC=∠BDC=60![]() ,∠DGC=∠DBC=60
,∠DGC=∠DBC=60![]() ,求得∠BGC=∠DGC=60
,求得∠BGC=∠DGC=60![]() ,过点C作CM⊥GB于M,CN⊥GD于N(如图1),推出S四边形BCDG=S四边形CMGN,于是得到S四边形CMGN=2S△CMG=2×
,过点C作CM⊥GB于M,CN⊥GD于N(如图1),推出S四边形BCDG=S四边形CMGN,于是得到S四边形CMGN=2S△CMG=2×![]() ×CG×
×CG×![]() CG=
CG=![]() CG2.
CG2.
①∵ABCD为菱形,
∴AB=AD,
∵AB=BD,
∴△ABD为等边三角形,
∴∠A=∠BDF=60![]() ,
,
又∵AE=DF,AD=BD,
∴△AED≌△DFB(SAS),故本选项正确;
②过点C作CM⊥GB于M,CN⊥GD于N(如图1),
则△CBM≌△CDN(AAS),
∴CN=CM,
∵CG=CG,
∴Rt△CNG≌Rt△CMG(HL),
∴∠DGC=∠BGC,
∴CG平分∠BGD;故本选项正确;
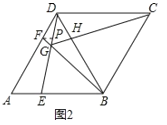
③过点F作FP∥AE交DE于P点(如图2),
∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=FP:2AE=1:6,
∵FP∥AE,
∴PF∥BE,
∴FG:BG=FP:BE=1:6,
即BG=6GF,
∴![]()
故本选项错误;
④∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60![]() =∠BCD,
=∠BCD,
即∠BGD+∠BCD=180![]() ,
,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60![]() ,∠DGC=∠DBC=60
,∠DGC=∠DBC=60![]() ,
,
∴∠BGC=∠DGC=60![]() ,
,
过点C作CM⊥GB于M,CN⊥GD于N(如图1),
则△CBM≌△CDN(AAS),
∴S四边形BCDG=S四边形CMGN,
S四边形CMGN=2S△CMG,
∵∠CGM=60![]() ,∴∠GCM=60
,∴∠GCM=60![]()
∴GM=![]() CG,CM=
CG,CM=![]() =
=![]() CG,
CG,
∴S四边形CMGN=2S△CMG=2×![]() ×
×![]() ×CG×
×CG×![]() CG=
CG=![]() CG2,故本选项正确;
CG2,故本选项正确;
故答案为:①②④.


科目:初中数学 来源: 题型:
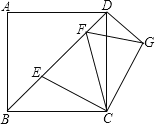
【题目】如图,在正方形ABCD中,AB=a,点E,F在对角线BD上,且∠ECF=∠ABD,将△BCE绕点C旋转一定角度后,得到△DCG,连接FG.则下列结论:
①∠FCG=∠CDG;
②△CEF的面积等于![]() ;
;
③FC平分∠BFG;
④BE2+DF2=EF2;
其中正确的结论是_____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=a![]() -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).
(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-![]() a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.
①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是8×8的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:
(1)在图1中画一个以线段AB为一边的正方形,并求出此正方形的面积;(所画正方形各顶点必须在小正方形的顶点上)
(2)在图2中画一个以线段AB为一边的等腰三角形,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为12.
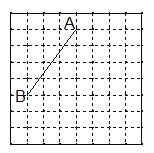

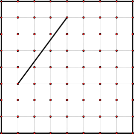
图1 图2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,抛物线![]() 过点
过点![]() ,点
,点![]() 是直线
是直线![]() 上方抛物线上的一动点,
上方抛物线上的一动点,![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,连接
,连接![]() ,交直线
,交直线![]() 于点
于点![]() .
.
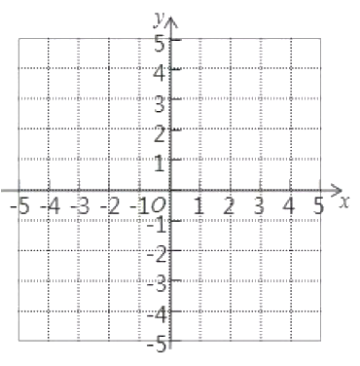
![]() 在如下坐标系作出该抛物线简图,并求抛物线的函数表达式;
在如下坐标系作出该抛物线简图,并求抛物线的函数表达式;
![]() 当
当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 求线段
求线段![]() 的最大值:
的最大值:
![]() 当线段
当线段![]() 最大时,若点
最大时,若点![]() 在直线
在直线![]() 上且
上且![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中我们经历了“确定函数的表达,利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.已知函数y=2![]() ﹣b的定义域为x≥﹣3,且当x=0时y=2
﹣b的定义域为x≥﹣3,且当x=0时y=2![]() ﹣2由此,请根据学习函数的经验,对函数y=2
﹣2由此,请根据学习函数的经验,对函数y=2![]() ﹣b的图象与性质进行如下探究:
﹣b的图象与性质进行如下探究:
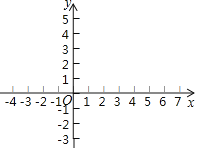
(1)函数的解析式为: ;
(2)在给定的平面直角坐标系xOy中,画出该函数的图象并写出该函数的一条性质: ;
(3)结合你所画的函数图象与y=x+1的图象,直接写出不等式2![]() ﹣b≤x+1的解集.
﹣b≤x+1的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
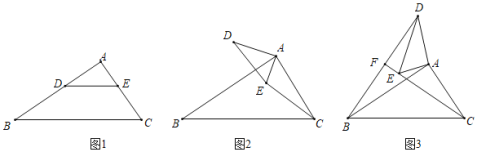
【题目】问题发现:
(1)如图1,在Rt△ABC中,∠A=90°,AB=kAC(k>1),D是AB上一点,DE∥BC,则BD,EC的数量关系为 .
类比探究
(2)如图2,将△AED绕着点A顺时针旋转,旋转角为a(0°<a<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由
拓展延伸:
(3)如图3,在(2)的条件下,将△AED绕点A继续旋转,旋转角为a(a>90°).直线BD,CE交于F点,若AC=1,AB=![]() ,则当∠ACE=15°时,BFCF的值为_____.
,则当∠ACE=15°时,BFCF的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
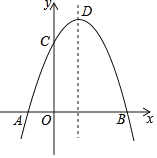
【题目】如图,抛物线y=﹣x2+2x+m交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=﹣1,则b=4;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2.
其中结论正确的序号是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com