
分析 (1)为关于x的一元二次方程kx2-6x+9=0有两个不相等的实数根,所以k≠0且△=b2-4ac>0,建立关于k的不等式组,解得k的取值范围即可;
(2)设方程的另一根为m,根据根与系数的关系,列方程组即可解得结果.
解答 解:(1)∵△=36-4k×9=36-36k>0,
∴k<1,
∵关于x的一元二次方程kx2-6x+9=0,k≠0,
∴k的取值范围为:k<1且k≠0;
(2)设方程的另一根为m,
∴$\left\{\begin{array}{l}{m+1=\frac{6}{k}}\\{m=\frac{9}{k}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-3}\\{k=-3}\end{array}\right.$,
∴k=-3,另一根为-3.
点评 本题考查了一元二次方程根的判别式的应用,根与系数的关系,方程的解,切记不要忽略一元二次方程二次项系数不为零这一隐含条件.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 2a-2b=2(a-b) | B. | x2-9=(x+3)(x-3) | C. | a2+4a-4=(a+2)2 | D. | -x2-x+2=-(x-1)(x+2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
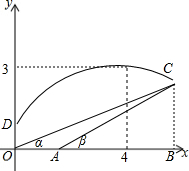 某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.
某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
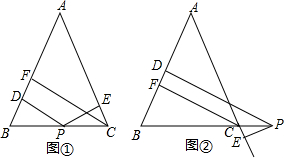 如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)
如图1,在△ABC中,AB=AC,在BC边上有任意一点P,则点P到AB,AC的距离之和等于AB边上的高,即PD+PE=CF,如图2,如果点P在BC的延长线上,那么请猜想点P到AB,AC的距离与AB边上的高的关系.(提示:用面积法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com