

 解:(1)∵△ABC是等边三角形,AB的长为a,
解:(1)∵△ABC是等边三角形,AB的长为a,| 60πa2 |
| 360 |
| 60πb2 |
| 360 |
| 1 |
| 6 |


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
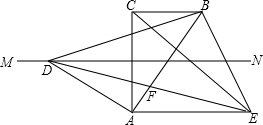 如图,在直角梯形ACBE中,BC∥AE,AC⊥AE,∠CAB=30°,AB=AE,作CA的垂直平分线MN交AB的垂线AD于D.
如图,在直角梯形ACBE中,BC∥AE,AC⊥AE,∠CAB=30°,AB=AE,作CA的垂直平分线MN交AB的垂线AD于D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,O为原点,每个小方格的边长为1个单位长度,在第一象限内有横、纵坐标均为整数的A、B两点,且OA=OB=
如图,在平面直角坐标系中,O为原点,每个小方格的边长为1个单位长度,在第一象限内有横、纵坐标均为整数的A、B两点,且OA=OB=| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一个水池的容积是8m2,如果从进水管中每小时流进x m2,那么经过y小时就可以把水池注满.
一个水池的容积是8m2,如果从进水管中每小时流进x m2,那么经过y小时就可以把水池注满.查看答案和解析>>
科目:初中数学 来源: 题型:
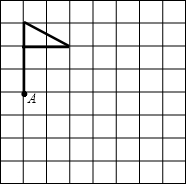 如图,方格中是美丽可爱的小彩旗图形,请将小彩旗向右平移四个单位(每小方格边长为1个单位),其中A点平移到A1位置,再将平移后以点A1为旋转中心顺时针方向旋转90°(只要求画出平移后的图形,不要求写出作图步骤和过程)
如图,方格中是美丽可爱的小彩旗图形,请将小彩旗向右平移四个单位(每小方格边长为1个单位),其中A点平移到A1位置,再将平移后以点A1为旋转中心顺时针方向旋转90°(只要求画出平移后的图形,不要求写出作图步骤和过程)查看答案和解析>>
科目:初中数学 来源: 题型:
| A、调查某种胶囊中铬的含量 |
| B、了解某班学生对影片《暮光之城》的关注度 |
| C、对我国首艘航空母舰“辽宁号”零件的检查 |
| D、调查重庆市民对“钓鱼岛”事件的态度 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com