
【题目】数学课上,潘老师给出如下定义:如果一个三角形有一边上的高线等于这条边的一半,那么称这个三角形为“垂美三角形”,这条边称为这个三角形的“垂美边”.
概念理解:
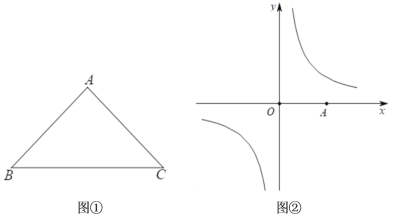
(1)如图①,已知∠A=90°,AB=AC,请证明等腰Rt△ABC一定是“垂美三角形”.
探索运用:
(2)已知等腰△ABC是“垂美三角形”,请求出顶角的度数.
能力提升:
(3)如图②,在直角坐标系中,点A为x轴正半轴上动点,在反比例函数![]() 的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
【答案】(1)证明见解析;(2)顶角为30°,90°或150°;(3)存在点B1(![]() ,1)、B2(-
,1)、B2(-![]() ,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边
,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边
【解析】
过点A作AH⊥BC于H,根据等腰三角形的三线合一即可求证;
分三种情况求∠BAC的度数:①若AB=AC,BC是“垂美边”; ②若BA=BC,BC是“垂美边”; ③若CA=CB,BC是“垂美边”
(3) 当△OAB是“垂美三角形”,且OA,OB均为“垂美边”,设△ABC的边OA、OB上的高分别记为ha、hb,则由“垂美三角形”的定义可知,ha=![]() OA, hb=
OA, hb=![]() OB.根据面积相等,得出OA=OB, ∠AOB的度数为30°或150°. 设B(m,
OB.根据面积相等,得出OA=OB, ∠AOB的度数为30°或150°. 设B(m,![]() )即可得出B点坐标
)即可得出B点坐标
(1)证明:如图,过点A作AH⊥BC于H.

∵AB=AC,
∴H是BC中点,
∵∠BAC=90°,
∴AH=![]() BC,
BC,
∴等腰Rt△ABC是“垂美三角形”.
(2)①如图,若AB=AC,BC是“垂美边”,过点A做AH⊥BC于H.

则AH=BH=CH,且AH⊥BC,
∴∠B=∠C=45°,
∴∠BAC=90°;
②如图,若BA=BC,BC是“垂美边”,过点A做AH⊥BC于H,
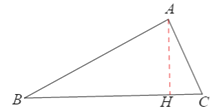
则BC=2AH=AB,且AH⊥BC,
∴∠B=30°;
③如图,若CA=CB,BC是“垂美边”,过点A做AH⊥BC交BC的延长线于H,
则BC=2AH=AC,且AH⊥BC,

∴∠ACD=30°,从而∠ACB=150°.
综上所述,顶角为30°,90°或150°.
(3)当△OAB是“垂美三角形”,且OA,OB均为“垂美边”,设△ABC的边OA、OB上的高分别记为ha、hb,则由“垂美三角形”的定义可知,ha=![]() OA, hb=
OA, hb=![]() OB.
OB.
而S△ABC=![]() OA
OA![]() ha=
ha=![]() OA
OA![]() hb,
hb,
∴OA=OB.
由(2)可知,∠AOB的度数为30°或150°.
设B(m,![]() )则由“垂美三角形”的定义有:
)则由“垂美三角形”的定义有:![]() =
=![]() OA,从而OA2=
OA,从而OA2=![]() .
.
又OB2=m2+![]() ,则有OA=OB可得:
,则有OA=OB可得: ![]() ,解得m=
,解得m=![]() .
.
故存在点B1(![]() ,1)、B2(-
,1)、B2(-![]() ,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边”.
,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边”.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y =-x+4与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且OA=![]() OB, 抛物线y =ax2+bx+4经过A,B,C三点.
OB, 抛物线y =ax2+bx+4经过A,B,C三点.
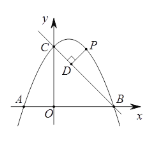
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作PD⊥BC,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值;
(3)设点E为抛物线对称轴与直线BC的交点,若A,B,E三点到同一直线的距离分别是d1,d2,d3,问是否存在直线l,使得d1= d2=![]() d3? 若存在,请直接写出d3的值,若不存在,请说明理由.
d3? 若存在,请直接写出d3的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm
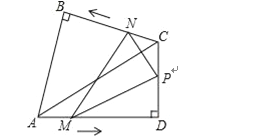
(1)填空:AD= (cm),DC= (cm)
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B方向运动,点N到AD的距离(用含x的式子表示)
(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.
(参考数据sin75°=![]() ,sin15°=
,sin15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李白笔下“孤帆一片日边来”描述了在喷薄而出的红日映衬下,远远望见一叶帆船驶来的壮美河山之境.聪明的小芬同学利用几何图形,构造出了此意境!如图半径为5的⊙0在线段AB上方,且圆心O在线段AB的中垂线上,到AB的距离为![]() ,已知AB=20.线段PQ在AB上(AP<AQ),PQ=6,以PQ的中点C为顶点向上作Rt△CDE,其中∠D=90°,CD=3,sin∠DCE=sin∠DCQ=
,已知AB=20.线段PQ在AB上(AP<AQ),PQ=6,以PQ的中点C为顶点向上作Rt△CDE,其中∠D=90°,CD=3,sin∠DCE=sin∠DCQ=![]() ,设AP=m,当边DE与⊙O有交点时,则m的取值范围是( )
,设AP=m,当边DE与⊙O有交点时,则m的取值范围是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班选举班干部,全班有40名同学都有选举权和被选举权,他们的编号分别为1,2,…,40.老师规定:同意某同学当选的记“1”,不同意(含弃权)的记“0”.
如果令
其中i=1,2,…,40;j=1,2,…,40.则a1,1a1,2+a2,1a2,2+a3,1a3,2+…+a40,1a40,2表示的实际意义是( )
A. 同意第1号或者第2号同学当选的人数
B. 同时同意第1号和第2号同学当选的人数
C. 不同意第1号或者第2号同学当选的人数
D. 不同意第1号和第2号同学当选的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:若存在实数m,当其自变量的值为m时,其函数值等于﹣m,则称﹣m为这个函数的反向值.在函数存在反向值时,该函数的最大反向值与最小反向值之差n称为这个函数的反向距离.特别地,当函数只有一个反向值时,其反向距离n为零.
例如,图中的函数有4,﹣1两个反向值,其反向距离n等于5.
(1)分别判断函数y=﹣x+1,y=![]() ,y=x2有没有反向值?如果有,直接写出其反向距离;
,y=x2有没有反向值?如果有,直接写出其反向距离;
(2)对于函数y=x2﹣b2x,
①若其反向距离为零,求b的值;
②若﹣1≤b≤3,求其反向距离n的取值范围;
(3)若函数y= 请直接写出这个函数的反向距离的所有可能值,并写出相应m的取值范围.
请直接写出这个函数的反向距离的所有可能值,并写出相应m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是Rt△ABC的AB边上一点,∠ACB=90°,⊙O与AC相切于点D,与边AB,BC分别相交于点E,F.
(1)求证:DE=DF;
(2)当BC=3,sinA=![]() 时,求AE的长.
时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣bx.
(1)若此抛物线与直线y=x只有一个公共点,且向右平移1个单位长度后,刚好过点(3,0).
①求此抛物线的解析式;
②以y轴上的点P(0,n)为中心,作该抛物线关于点P对称的抛物线y',若这两条抛物线有公共点,求n的取值范围;
(2)若a>0,将此抛物线向上平移c个单位(c>0),当x=c时,y=0;当0<x<c时,y>0.试比较ac与1的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com