
分析 (1)进行判别式的值得到△=4m2+1,利用非负数的性质得△>0,然后根据判别式的意义可判断方程总有两个不相等的实数根;
(2)令m=0时,则方程化为x2-x=0,然后利用因式分解法解方程.
解答 (1)证明:△=(2m+1)2-4m=4m2+1,
∵4m2≥0,
∴△>0,
∴方程总有两个不相等的实数根;
(2)解:当m=0时,方程化为x2-x=0,
解得x1=0,x2=1.
点评 本题考查了根与系数的关系:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 累计实验次数 | 100 | 200 | 300 | 400 | 500 |
| 顶尖朝上次数 | 55 | 109 | 161 | 211 | 269 |
| 顶尖朝上频率 | 0.550 | 0.545 | 0.536 | 0.528 | 0.538 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
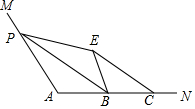 如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=70°.
如图,∠A=110°,在边AN上取B,C,使AB=BC.点P为边AM上一点,将△APB沿PB折叠,使点A落在角内点E处,连接CE,则∠BPE+∠BCE=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com