
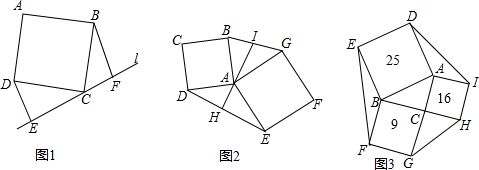
分析 (1)根据全等三角形的判定证明即可;
(2)由(1)可知:△DAH≌△ABM,△EAH≌△AGN,从而可知:BM=AH=GN,然后再证明△BIM≌△GIN,从而可得到BI=BI;
(3)由全等三角形的性质可知S△ADE=S△ABG,然后用上述结论可知△BEF、△GCH,△ADI的面积都等于△ACB的面积,从而可求得答案.
解答 证明:(1)∵四边形ABCD是正方形,
∴DC=BC,∠DCB=90°,
∴∠DCE+∠BCF=90°,
∵DE⊥CE,BF⊥CF,
∴∠DCE+∠EDC=90°,
∴∠BCF=∠EDC,
同理∠DCE=∠CBF,
在△DCE与△CBF中,
$\left\{\begin{array}{l}{∠DCE=∠CBF}\\{∠BCF=∠EDC}\\{DC=BC}\end{array}\right.$,
∴△DCE≌△CBF(AAS);
(2)过点B作BM⊥AI于点M,过点G作GN⊥AI交延长线于点N,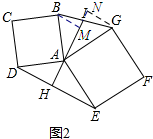
由(1)可知:△DAH≌△ABM、△AHE≌△GNA,
∴BM=AH,GN=AH.
∴BM=GN.
在△BMI和△GNI中,
$\left\{\begin{array}{l}{∠BMA=∠GNA}\\{∠BMI=∠GNI}\\{BM=NG}\end{array}\right.$,
∴△BMI≌△GNI.
∴BI=GI.
(3)∵△DAH≌△ABM、△AHE≌△GNA,
∴S△ADE=S△ABM+S△ANG.
∵△BMI≌△GNI,
∴S△BMI=S△GNI.
∴S△ADE=S△ABG.
∴${S}_{△BEF}={S}_{△CGH}={S}_{△ADI}={S}_{△ABC}=\frac{1}{2}×3×4=6$.
∴六边形的面积=25+16+9+4×6=74.
点评 本题主要考查的是全等三角形的性质和判定,发现问题的结论,并利用问题的结论进行证明是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 若点O为直线AB上一点,OC为射线,OE平分∠AOC,OF平分∠BOC.
若点O为直线AB上一点,OC为射线,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明从A地出发,途中经过C地,后到达B地,到达B地后,立即原路返回,他距A地的距离S(千米)和所用时间t(小时)之间的函数关系如图所示,若小明前后两次经过点C时间相差2$\frac{1}{3}$小时,那么A、C两地之间距离为140千米.
小明从A地出发,途中经过C地,后到达B地,到达B地后,立即原路返回,他距A地的距离S(千米)和所用时间t(小时)之间的函数关系如图所示,若小明前后两次经过点C时间相差2$\frac{1}{3}$小时,那么A、C两地之间距离为140千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com