
已知:o为坐标原点,∠ AOB=300 , ∠ABO=900 且A(2,0)

求: 过A、B、O三点的二次函数解析式
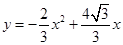
【解析】本题考查了用待定系数法求二次函数解析式的方法.关键是根据条件确定抛物线解析式的形式,再求其中的待定系数.一般式:y=ax2+bx+c(a≠0);顶点式y=a(x-h)2+k,其中顶点坐标为(h,k);交点式y=a(x-x1)(x-x2),抛物线与x轴两交点为(x1,0),(x2,0).
过B点作BC⊥OA,垂足为C,解Rt△OAB可求OB,解Rt△OBC可求OC、BC,确定B点坐标,根据O、A、B三点坐标,设交点式求二次函数解析式
解:过B点作BC⊥OA,垂足为C,
在Rt△OAB中,OA=2,∠AOB=30°,
∴OB= ,
,
在Rt△OBC中,OB= ,∠BOC=30°,
,∠BOC=30°,
∴OC= ,BC=
,BC=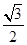 ,
,
即B( ,
,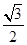 ),
),
∵抛物线过O(0,0),A(2,0),
设抛物线解析式为y=ax(x-2),将B( ,
,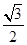 )代入,得
)代入,得

解得a=- ,
,
∴二次函数解析式为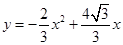


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 3 |
| ||
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).
如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).
如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com