
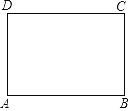
【题目】如图,已知矩形纸片ABCD,怎样折叠,能使边AB被三等分?
以下是小红的研究过程.
思考过程 | 要使边AB被三等分,若从边DC上考虑,就是要折出DM= 也就是要折出DM= 当DB、AM相交于F时,即要折出对角线上的DF= |
折叠方法和示意图 | ①折出DB;对折纸片,使D、B重合,得到的折痕与DB相交于点E;继续折叠纸片,使D、B与E重合,得到的折痕与DB分别相交于点F、G; ②折出AF、CG,分别交边CD、AB于M、Q; ③过M折纸片,使D落在MC上,得到折痕MN,则边AB被N、Q三等分.
|
(1)整理小红的研究过程,说明AN=NQ=QB;
(2)用一种与小红不同的方法折叠,使边AB被三等分.(需简述折叠方法并画出示意图)
【答案】(1)见解析;(2)见解析
【解析】
(1)由折叠的性质可得DF=![]() DB,DM=AN,通过证明
DB,DM=AN,通过证明![]() DFM∽
DFM∽![]() BAF,可得DM=
BAF,可得DM=![]() AB,可得AN=
AB,可得AN=![]() AB,同理可求QB=
AB,同理可求QB=![]() AB,可得结论;
AB,可得结论;
(2)所求图形,如图所示,由折叠的性质可得AF=BF=DE=EC=![]() CD,AN=DM=NQ,通过证明
CD,AN=DM=NQ,通过证明![]() AGF∽
AGF∽![]() CGD,可得
CGD,可得![]() ,由平行线分线段成比例可得AN=
,由平行线分线段成比例可得AN=![]() MC=DM,即可证AN=NQ=QB.
MC=DM,即可证AN=NQ=QB.
解:(1)由折叠的性质可得,DF=![]() DB,四边形ADMN是矩形,
DB,四边形ADMN是矩形,
∴DM=AN,
∵CD∥AB,
∴![]() DFM∽
DFM∽![]() BAF,
BAF,
∴![]() =
=![]() ,
,
∴DM=![]() AB,
AB,
∴AN=![]() AB,
AB,
同理可求QB=![]() AB,
AB,
∴AN=NQ=QB;
(2)如图,
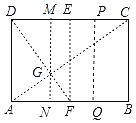
①将矩形ABCD对折,使AD与BC重合,折痕为EF;
②连接AC,DF,交点为G,
③过点G折叠矩形ABCD,使点D落在CE上,对应点为E,
使点A落在BF上,对应点为Q,折痕为MN;
∴点N,点Q为AB的三等分点.
理由如下:由折叠的性质可得:AF=BF=DE=EC=![]() CD,AN=DM=NQ,
CD,AN=DM=NQ,
∵AB∥CD,
∴![]() AGF∽
AGF∽![]() CGD,
CGD,
∴![]() ,
,
∵AB∥CD,
∴![]() ,
,
∴AN=![]() MC=DM,
MC=DM,
∴AN=DM=![]() CD=
CD=![]() AB,
AB,
∴NQ=![]() AB,
AB,
∴AN=NQ=QB.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】如图1,在三角形纸板![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一个点(不与点
上的一个点(不与点![]() 重合),沿
重合),沿![]() 折叠纸板,点
折叠纸板,点![]() 的对应点是点
的对应点是点![]() .
.
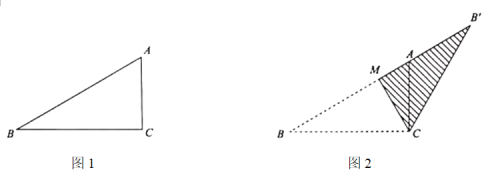
(1)如图2,当点![]() 在射线
在射线![]() 上时,
上时,![]() ________°.
________°.
(2)若![]() ,且点
,且点![]() 不在直线
不在直线![]() 右侧,则点
右侧,则点![]() 到
到![]() 的距离是__________
的距离是__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
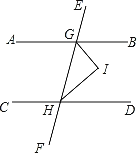
【题目】如图,已知AB∥CD,直线EF分别交直线AB、CD于点G、H,GI、HI分别平分∠BGH、∠GHD.
(1)求证GI⊥HI.
(2)请用文字概括(1)所证明的命题: .
查看答案和解析>>
科目:初中数学 来源: 题型:
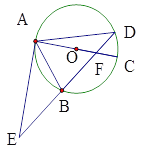
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑行是现在流行的健身方式之一,周末“绿色骑行俱乐部”组织了一次从甲地出发,目的地为乙地的骑行活动,在“俱乐部”自行车队出发1小时后,恰有一辆摩托车从甲地出发,沿自行车队行进路线前往乙地,到达乙地后立即按原路返回甲地.自行车队与摩托车行驶速度均保持不变,并且摩托车行驶速度是自行车队行驶速度的3倍.如图所示的是自行车队、摩托车离甲地的路程![]() 与自行车队离开甲地的时间
与自行车队离开甲地的时间![]() 的关系图象,请根据图象提供的信息,回答下列问题.
的关系图象,请根据图象提供的信息,回答下列问题.
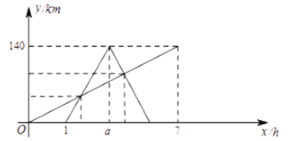
(1)摩托车行驶的速度是__________;![]() ____________;
____________;
(2)求出自行车队离甲地的路程![]() 与自行车队离开甲地的时间
与自行车队离开甲地的时间![]() 的关系式,并求出自行车队出发多少小时与摩托车相遇;
的关系式,并求出自行车队出发多少小时与摩托车相遇;
(3)直接写出当摩托车与自行车队相距![]() 时,此时离摩托车出发经过了多少小时.
时,此时离摩托车出发经过了多少小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 是一条对角线,点
是一条对角线,点![]() 在直线
在直线![]() 上(不与点
上(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,平移
,平移![]() ,使点
,使点![]() 移动到点
移动到点![]() ,得到
,得到![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,![]() .
.
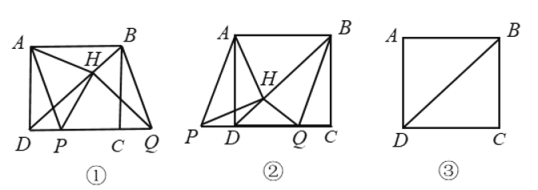
(问题发现)
(1)如图①,若点![]() 在线段
在线段![]() 上,
上,![]() 与
与![]() 的数量关系是________,位置关系是________.
的数量关系是________,位置关系是________.
(拓展探究)
(2)如图②,若点![]() 在线段
在线段![]() 的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明,否则说明理由.
(解决问题)
(3)若点![]() 在线段
在线段![]() 的延长线上,且
的延长线上,且![]() ,正方形
,正方形![]() 的边长为2,请直接写出求
的边长为2,请直接写出求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②9a+3b+c=0;③若点
;②9a+3b+c=0;③若点![]() ,点
,点![]() 是此函数图象上的两点,则
是此函数图象上的两点,则![]() ;④
;④![]() .其中正确的个数( )
.其中正确的个数( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com