【题目】有3张扑克牌，分别是红桃3、红桃4和黑桃5．把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张．
（1）先后两次抽得的数字分别记为x和y，画出树形图或列表求|x﹣y|≥1的概率．
（2）甲、乙两人做游戏，现有两种方案．A方案：若两次抽得相同花色则甲胜，否则乙胜．B方案：若两次抽得数字和为奇数则甲胜，否则乙胜．请问甲选择哪种方案胜率更高？
【答案】（1）
；（2）甲选择A方案胜率更高，理由见解析
【解析】
(1)列出表格,再根据概率公式计算即可.
(2)根据题意分别列出两种方案的所有情况,算出概率比较即可.
（1）列表如下：
红桃3 | 红桃4 | 黑桃5 | |
红桃3 | （红桃3，红桃3） | （红桃4，红桃3） | （黑桃5，红桃3） |
红桃4 | （红桃3，红桃4） | （红桃4，红桃4） | （黑桃5，红桃4） |
黑桃5 | （红桃3，黑桃5） | （红桃4，黑桃5） | （黑桃5，黑桃5） |
所有等可能的情况有9种，其中|x﹣y|≥1的情况有6种，
则P＝
＝；
（2）A方案：两次抽得相同花色的情况有5种，不同花色的情况有4种，
则P（甲获胜）＝
，P（乙获胜）＝
；
B方案：两次抽得数字和为奇数的情况有4种，偶数的情况有5种，
则P（甲获胜）＝，P（乙获胜）＝，
则甲选择A方案胜率更高．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】为了解盐渎街道
～
岁居民最喜欢的春节晚会节目类型，某兴趣小组对街道内该年龄段部分居民展开了随机问卷调查（每人只能选择其中一项），并将调查数据整理后绘成如下两幅不完整的统计图. 请根据图中信息解答下列问题：
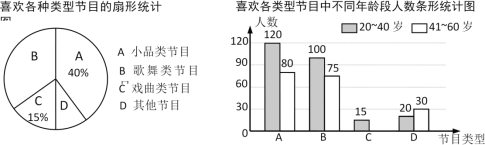
（1）求参与问卷调查的总人数；
（2）补全条形统计图，并求出扇形
的圆心角；
（3）该街道～岁的居民约
人，估算这些人中最喜欢歌舞类节目的人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知函数
的图象与
轴交于点A，与函数
的图象交于C、D两点，以OC、OD为邻边作平行四边形OCED.下列结论中：①OC=OD；②若
，则当
时，
；③若，则平行四边形OCED的面积为3；④若∠COD=45°，则.其中正确的有（ ）
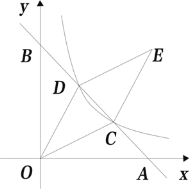
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，过⊙T外一点P引它的两条切线，切点分别为M，N，若
，则称P为⊙T的环绕点．
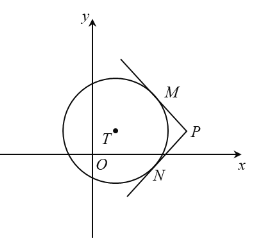
(1)当⊙O半径为1时，
①在
中，⊙O的环绕点是_________;
②直线y=2x+b与x轴交于点A，y轴交于点B，若线段AB上存在⊙O的环绕点，求b的取值范围；
(2)⊙T的半径为1，圆心为（0，t），以
为圆心，
为半径的所有圆构成图形H，若在图形H上存在⊙T的环绕点，直接写出t的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，用一段长为30m的篱笆围成一个一边靠墙的矩形菜园（矩形ABCD），墙长为22m，这个矩形的长AB＝xm，菜园的面积为Sm2，且AB＞AD．
（1）求S与x之间的函数关系式，并写出自变量x的取值范围．
（2）若要围建的菜园为100m2时，求该莱园的长．
（3）当该菜园的长为多少m时，菜园的面积最大？最大面积是多少m2？
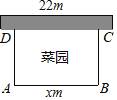
查看答案和解析>>
科目：初中数学 来源： 题型：
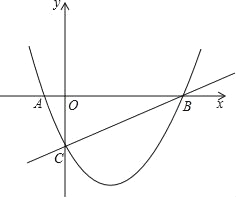
【题目】如图，已知抛物线y=ax2﹣
x+c与x轴相交于A、B两点，并与直线y=
x﹣2交于B、C两点，其中点C是直线y=x﹣2与y轴的交点，连接AC．
（1）求抛物线的解析式；
（2）证明：△ABC为直角三角形；
（3）△ABC内部能否截出面积最大的矩形DEFG？（顶点D、E、F、G在△ABC各边上）若能，求出最大面积；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：△AOB和△COD均为等腰直角三角形，∠AOB＝∠COD＝90°．连接AD，BC，点H为BC中点，连接OH．
（1）如图1所示，若AB＝8，CD＝2，求OH的长；
（2）将△COD绕点O旋转一定的角度到图2所示位置时，线段OH与AD有怎样的数量和位置关系，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y＝ax2+bx+5与x轴交于A（﹣1，0），B（5，0）两点（点A在点B的左侧），与y轴交于点C．
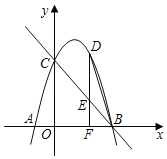
（1）求抛物线的解析式；
（2）点D是第一象限内抛物线上的一个动点（与点C，B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD，直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．
（3）若M为抛物线对称轴上一动点，使得△MBC为直角三角形，请直接写出点M的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
