

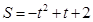
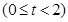 ,当
,当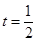 时,S的值最大;(3)存在,点M的坐标为(1,0)或(2,0),理由见试题解析.
时,S的值最大;(3)存在,点M的坐标为(1,0)或(2,0),理由见试题解析.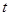 秒时,NB=
秒时,NB=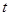 ,OM=
,OM=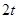 ,则CN=
,则CN=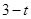 ,AM=
,AM=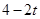 ,∵A(4,0),C(0,4),∴AO=CO=4,∵∠AOC=90°,∴∠BCA=∠MAQ=45°,∴QN=CN=
,∵A(4,0),C(0,4),∴AO=CO=4,∵∠AOC=90°,∴∠BCA=∠MAQ=45°,∴QN=CN=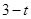 ,∴PQ=
,∴PQ=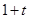 ,
,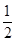 AM•PQ=
AM•PQ=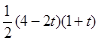 =
=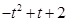 .∴
.∴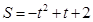 ,∴
,∴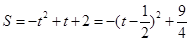 ,∵
,∵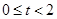 ,∴当
,∴当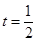 时,S的值最大.
时,S的值最大.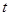 秒时,NB=
秒时,NB=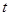 ,OM=
,OM=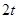 ,则CN=
,则CN=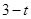 ,AM=
,AM=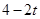 ,∴∠BCA=∠MAQ=45°.
,∴∠BCA=∠MAQ=45°.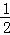 MA,
MA,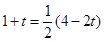 ,∴
,∴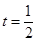 ,∴点M的坐标为(1,0).
,∴点M的坐标为(1,0).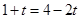 ,解得:
,解得: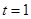 ,∴点M的坐标为(2,0).
,∴点M的坐标为(2,0).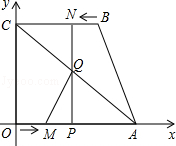


科目:初中数学 来源:不详 题型:解答题
 2,4) 和点B (1,0)都在抛物线
2,4) 和点B (1,0)都在抛物线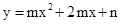 上.
上.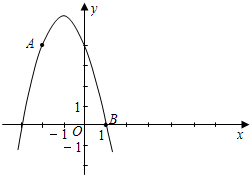
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
速度 (千米/时) (千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | … |
刹车距离 (米) (米) | 0 |  | 2 |  | 6 |  | … |
 作为点的坐标,在如图所示的坐标系中画出刹车距离
作为点的坐标,在如图所示的坐标系中画出刹车距离 (米)与速度
(米)与速度 (千米/时)的函数图象,并求函数的解析式;
(千米/时)的函数图象,并求函数的解析式;
 (米)与速度
(米)与速度 (千米/时)满足函数
(千米/时)满足函数 ,请你就两车速度方面分析相撞原因.
,请你就两车速度方面分析相撞原因. 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
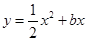 与直线
与直线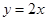 交于点
交于点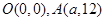 .点
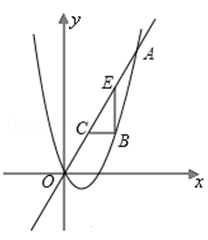
.点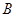 是抛物线上
是抛物线上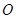 ,
,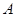 之间的一个动点,过点
之间的一个动点,过点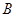 分别作
分别作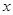 轴、
轴、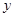 轴的平行线与直线
轴的平行线与直线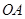 交于点
交于点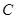 ,
,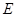 .
.
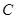 的横坐标为2,求
的横坐标为2,求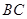 的长;
的长;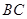 ,
,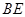 为边构造矩形
为边构造矩形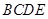 ,设点
,设点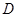 的坐标为
的坐标为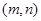 ,求出
,求出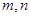 之间的关系式.
之间的关系式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
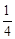 ).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).
).将抛物线C1向下平移h个单位(h>0)得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点(如图),且点A、C关于y轴对称,直线AB与x轴的距离是m2(m>0).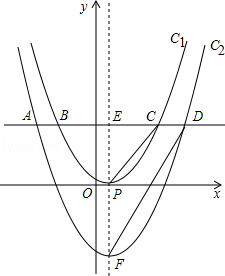
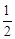 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 B、
B、 C、
C、 D、
D、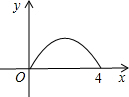
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com