
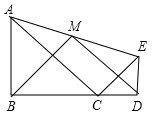
【题目】如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=![]() ;②S△ABC+S△CDE≧S△ACE;③BM⊥DM;④BM=DM,正确结论的个数是( )
;②S△ABC+S△CDE≧S△ACE;③BM⊥DM;④BM=DM,正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
试题解析:∵△ABC和△CDE均为等腰直角三角形,
∴AB=BC,CD=DE,
∴∠BAC=∠BCA=∠DCE=∠DEC=45°,
∴∠ACE=90°;
∵△ABC∽△CDE
∴![]()
①∴tan∠AEC=![]() ,
,
∴tan∠AEC=![]() ;故本选项正确;
;故本选项正确;
②∵S△ABC=![]() a2,S△CDE=
a2,S△CDE=![]() b2,S梯形ABDE=
b2,S梯形ABDE=![]() (a+b)2,
(a+b)2,
∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab,
S△ABC+S△CDE=![]() (a2+b2)≥ab(a=b时取等号),
(a2+b2)≥ab(a=b时取等号),
∴S△ABC+S△CDE≥S△ACE;故本选项正确;
④过点M作MN垂直于BD,垂足为N.
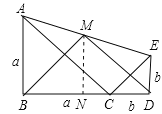
∵点M是AE的中点,
则MN为梯形中位线,
∴N为中点,
∴△BMD为等腰三角形,
∴BM=DM;故本选项正确;
③又MN=![]() (AB+ED)=
(AB+ED)=![]() (BC+CD),
(BC+CD),
∴∠BMD=90°,
即BM⊥DM;故本选项正确.
故选D.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个自由转动的转盘如图所示,一个分为![]() 等份,分别标有数字
等份,分别标有数字![]() ,
,![]() ,
,![]() ,另一个分为
,另一个分为![]() 等份,分别标有数字
等份,分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() .转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面
.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面![]() ,
,![]() 两种方案中选一种:方案
两种方案中选一种:方案![]() :猜“奇数”或猜“偶数”其中的一种;方案
:猜“奇数”或猜“偶数”其中的一种;方案![]() :猜“是
:猜“是![]() 的整数倍”或猜“不是
的整数倍”或猜“不是![]() 的整数倍”其中的一种.
的整数倍”其中的一种.
![]() 如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种方案,猜该种方案中的哪一种情况?请说明理由;
如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种方案,猜该种方案中的哪一种情况?请说明理由;
![]() 为了保证参与游戏双方的公平性,你应选择哪种猜数的方案?为什么?
为了保证参与游戏双方的公平性,你应选择哪种猜数的方案?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
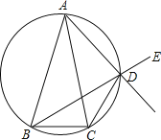
(1)求证:AD的延长线平分∠CDE;
(2)若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
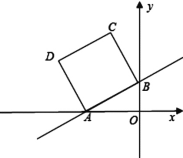
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)在x轴上找一点M,使△MDB的周长最小,请求出M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角尺ABC和ADE如图摆放,∠CAB=∠DAE=90°,∠ACB=∠DEA=30°,使点D落在BC边上,连结EB,EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③EB平分∠AED;④△ACE为等边三角形.其中正确的是( )
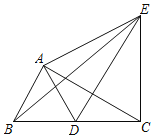
A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
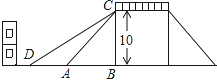
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将量角器和含![]() 角的一块直角三角板紧靠着放在同一平面内,使
角的一块直角三角板紧靠着放在同一平面内,使![]() ,
,![]() ,
,![]() 在一条直线上,且
在一条直线上,且![]() ,过点
,过点![]() 作量角器圆弧所在圆的切线,切点为
作量角器圆弧所在圆的切线,切点为![]() ,如果
,如果![]() ,则
,则![]() 的长是________
的长是________![]() .
.
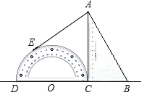
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
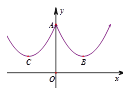
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com