
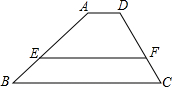
 如图,在四边形ABCD中,AD∥BC,E、F分别在AB、CD上,AD=2,AB=9,CD=6,BC=7,若EF∥BC,且四边形AEFD与四边形EBCF是周长相等,求EF的长.
如图,在四边形ABCD中,AD∥BC,E、F分别在AB、CD上,AD=2,AB=9,CD=6,BC=7,若EF∥BC,且四边形AEFD与四边形EBCF是周长相等,求EF的长. 分析 根据两梯形的周长相等可得AD+AE+EF+FD=EF+EB+BC+CF继而可得:AD+AE+FD=EB+BC+CF=$\frac{1}{2}$(AB+BC+CD+AD)=12,设$\frac{AE}{EB}$=k,则AE,DF,都可用k表示出来,从而可得出k的值,再运用平行的性质即可解出EF的长.
解答 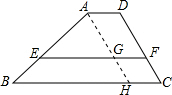 解:由已知AD+AE+EF+FD=EF+EB+BC+CF,
解:由已知AD+AE+EF+FD=EF+EB+BC+CF,
∴AD+AE+FD=EB+BC+CF=$\frac{1}{2}$(AB+BC+CD+AD)=12,
∵EF∥BC,
∴EF∥AD,$\frac{AE}{EB}$=$\frac{DF}{FC}$
设$\frac{AE}{EB}$=k,则AE=$\frac{k}{k+1}$AB=$\frac{9k}{k+1}$,DF=$\frac{k}{k+1}$CD=$\frac{6k}{k+1}$,
∴AD+AE+FD=2+$\frac{9k}{k+1}$+$\frac{6k}{k+1}$=12,
解得:k=2,
作AH∥CD,AH交BC于H,交EF于G,
则GF=HC=AD=2,BH=BC-CH=7-2=5,
∵$\frac{EG}{BH}$=$\frac{AE}{AB}$=$\frac{6}{9}$=$\frac{2}{3}$,
∴EG=$\frac{10}{3}$,
∴EF=EG+GF=$\frac{16}{3}$.
点评 本题考查了平行线分线段成比例,梯形的性质,熟练掌握平行线分线段成比例定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
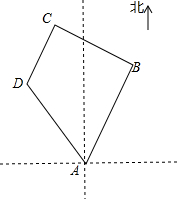 测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题
测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
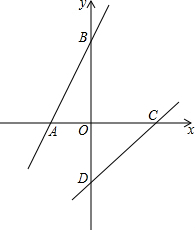 直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.
直线y=x+3分别交x轴、y轴于A、B两点,直线y=x-2分别交x轴、y 轴于C、D两点,在直线AB上是否存在一点P,使得S△PAD=S△PCD?若存在请求P点坐标,若不存在请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com