
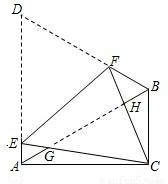
 ,AB=2;
,AB=2; ;
; ,EC=
,EC= ,
, =
= ;
; .
.

科目:初中数学 来源:2010年江苏省无锡市北片区中考数学一模试卷(解析版) 题型:解答题
 .
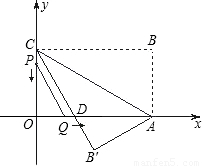
.
查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市北片区中考数学一模试卷(解析版) 题型:解答题
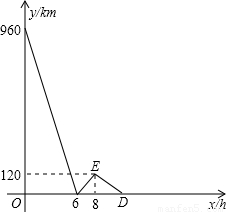
查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市北片区中考数学一模试卷(解析版) 题型:解答题
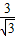 +(
+( )-1+(-1)2009(结果保留根号);
)-1+(-1)2009(结果保留根号);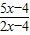 =
=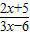 -
- ;
; ,其中a的值从不等式组
,其中a的值从不等式组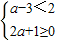 的解集中选取一个你认为合适的整数.
的解集中选取一个你认为合适的整数.查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市北片区中考数学一模试卷(解析版) 题型:填空题
 ,圆心P在函数y=
,圆心P在函数y=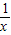 (x>0)的图象上运动,当⊙P与坐标轴相切时,点P的坐标为 .
(x>0)的图象上运动,当⊙P与坐标轴相切时,点P的坐标为 .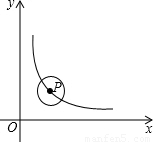
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com