Question

19．已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点O．点E从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点F从点C出发，沿CD方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接EO并延长，交BC于点G，．设运动时间为t（s）（0＜t＜6），解答下列问题：
（1）在运动的过程中，四边形EGCD的面积是否发生变化，请说明理由；如果不变化，并请求出四边形EGCD的面积；
（2）当t为何值时，△AOE是等腰三角形？
（3）连接EF，在运动过程中，是否存在某一时刻t，使EF与BD垂直？请说明理由．
（4）连接OF，在运动过程中，是否存在某一时刻t，使OC平分∠GOF？若存在，直接写出t的值；若不存在，请说明理由．

Answer 1

分析 （1）根据△AOE≌△COG可知，AE=CG，故CG+ED=AE+ED=AD（定值），据此判断即可；
（2）当△AOE是等腰三角形时，分三种情况进行讨论：当AE=AO时；当AE=OE时；当AO=OE时，分别进行判断即可；
（3）当EF与BD垂直时，根据△DEF∽△ABD，列出比例式求得t的值，判断是否符合0＜t＜6即可；
（4）过点C作CH⊥EG于H，作CM⊥OF于M，构造正方形HCMO，并求得其边长，再过点O作OP⊥BC于P，构造相似三角形，求得GH的长，最后在Rt△HCG中根据勾股定理，列出关于t的方程，求得t的值即可．

解答 解：（1）不变化
在矩形ABCD中，AO=CO，∠EAO=∠GCO，
又∵∠AOE=∠COG，
∴△AOE≌△COG（ASA），
∴AE=CG，
∴梯形形EGCD的面积
=（CG+ED）×CD×$\frac{1}{2}$
=（AE+ED）×CD×$\frac{1}{2}$
=8×6×$\frac{1}{2}$
=24，
故为四边形EGCD的面积为定值24；

（2）①当AE=AO时，△AOE是等腰三角形，
此时，AE=AO=$\frac{1}{2}$AC=$\frac{1}{2}$×$\sqrt{{6}^{2}+{8}^{2}}$=$\frac{1}{2}$×10=5，
∴t=5÷1=5（秒）；
②当AE=OE时，△AOE是等腰三角形，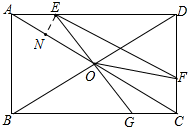
此时，过E作EN⊥AO于N，则AN=$\frac{1}{2}$AO=$\frac{5}{2}$，
由△AEN∽△ACD可得，$\frac{\frac{5}{2}}{t}=\frac{8}{10}$，
解得t=$\frac{25}{8}$；
③当AO=OE时，点E与点D重合，AE=8，
t=8÷1=8（秒）＞6（秒）（不合题意，舍去），
综上，当t为5或$\frac{25}{8}$秒时，△AOE是等腰三角形；

（3）不存在
理由：DE=AD-AE=8-t，DF=CD-CF=6-t，
当EF与BD垂直时，△DEF∽△ABD，
此时，$\frac{DE}{AB}$=$\frac{DF}{AD}$，即$\frac{8-t}{6}$=$\frac{6-t}{8}$，
解得t=14＞6（不合题意，舍去），
∴在运动过程中，不存在某一时刻t，使EF与BD垂直；

（4）存在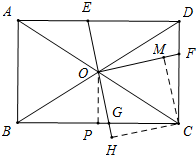
理由：如图，过点C作CH⊥EG于H，作CM⊥OF于M，
∵当OC平分∠GOF时，CH=CM，
又∵CG=AE=CF=t，
∴Rt△CGH≌Rt△CFM（HL），
∴∠HCG=∠MCF，
又∵∠MCG+∠MCF=90°，
∴∠HCG+∠MCF=90°，即∠HCM=90°，
∴四边形HCMO是矩形，
又∵CH=CM，
∴四边形HCMO是正方形，
∵OC=5，∠H=90°，
∴CH=$\frac{5}{\sqrt{2}}$=$\frac{5}{2}\sqrt{2}$，
过点O作OP⊥BC于P，则OP=$\frac{1}{2}$CD=3，PC=$\frac{1}{2}$BC=4，PG=4-t，
由△OPG∽△CHG可得，
$\frac{PG}{HG}$=$\frac{PO}{HC}$，即$\frac{4-t}{GH}$=$\frac{3}{\frac{5}{2}\sqrt{2}}$，
解得GH=$\frac{5\sqrt{2}（4-t）}{6}$，
∵在Rt△HCG中，HG²+HC²=GC²，
∴[$\frac{5\sqrt{2}（4-t）}{6}$]²+（$\frac{5}{2}\sqrt{2}$）²=t²，
解得t₁=$\frac{25}{7}$，t₂=$\frac{175}{7}$（不合题意，舍去），
∴在运动过程中，当t=$\frac{25}{7}$秒时，OC平分∠GOF．

点评 本题主要考查了四边形的综合应用，在解决有关等腰三角形的问题是往往需要进行分类讨论，分类时注意不能重复也不能遗漏．此外，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边、对顶角等隐含条件，以充分发挥基本图形的作用．