
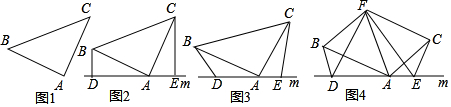
���� ��1���ٷ�����֤��������BD��ֱ��m��CE��ֱ��m�á�BDA=��CEA=90�㣬����BAC=90�㣬���ݵȽǵ������ȵá�CAE=��ABD��Ȼ����ݡ�AAS�����жϡ�ADB�ա�CEA����AE=BD��AD=CE�����ɵó����ۣ���ͬ��ķ������ɣ�
�ڸ���BD��ֱ��m��CE��ֱ��m�á�BDA=��CEA=90�㣬����BAC=90�㣬���ݵȽǵ������ȵá�CAE=��ABD��Ȼ����ݡ�AAS�����жϡ�ADB�ա�CEA����AE=BD��AD=CE������DE=AE+AD=BD+CE��
��2�����á�BDA=��BAC=�������DBA+��BAD=��BAD+��CAE=180��-�����ó���CAE=��ABD�������ó���ADB�ա�CEA���ɵó��𰸣�
��3���ɡ�ABF�͡�ACF��Ϊ�ȱ������Σ��õ�BAC=��BAF+��CAF=120�㣬���á�BDA=��BAC=120�㣬���DBA+��BAD=��BAD+��CAE=60�㣬�ó���CAE=��ABD�������ó���ADB�ա�CEA������ȫ�������ε����ʵõ�AE=BD����ABD=��CAE���õ���DBF=��FAE������ȫ�������ε����ʵõ�DF=EF����BFD=��AFE�����ݵõ�����
��� ֤������1���٢���ͼ1��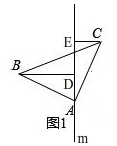 �ڡ�BD��ֱ��m��CE��ֱ��m��
�ڡ�BD��ֱ��m��CE��ֱ��m��
���BDA=��CEA=90�㣬
�ߡ�BAC=90�㣬
���BAD+��CAE=90�㣬
�ߡ�BAD+��ABD=90�㣬
���CAE=��ABD��
�ڡ�ADB�͡�CEA�У�$\left\{\begin{array}{l}{��ABD=��CAE}\\{��BDA=��CEA}\\{AB=AC}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��AE=BD��AD=CE��
��DE=AE-AD=BD-CE��
����ͼ1-1��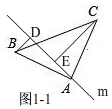
��BD��ֱ��m��CE��ֱ��m��
���BDA=��CEA=90�㣬
�ߡ�BAC=90�㣬
���BAD+��CAE=90�㣬
�ߡ�BAD+��ABD=90�㣬
���CAE=��ABD��
�ڡ�ADB�͡�CEA�У�$\left\{\begin{array}{l}{��ABD=��CAE}\\{��BDA=��CEA}\\{AB=AC}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��AE=BD��AD=CE��
��DE=AD-AE=CE-BD��
�������������DE=|BD-CE|��
�ʴ�Ϊ����=����DE=BD+CE��
�ڡ�BD��ֱ��m��CE��ֱ��m��
���BDA=��CEA=90�㣬
�ߡ�BAC=90�㣬
���BAD+��CAE=90�㣬
�ߡ�BAD+��ABD=90�㣬
���CAE=��ABD��
�ڡ�ADB�͡�CEA�У�$\left\{\begin{array}{l}{��ABD=��CAE}\\{��BDA=��CEA}\\{AB=AC}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE��
��2���ߡ�BDA=��BAC=����
���DBA+��BAD=��BAD+��CAE=180��-����
���CAE=��ABD��
�ڡ�ADB�͡�CEA�У�$\left\{\begin{array}{l}{��ABD=��CAE}\\{��BDA=��CEA}\\{AB=AC}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE��
��3���ߡ�ABF�͡�ACF��Ϊ�ȱ������Σ�
��BAC=��BAF+��CAF=120�㣬
���BDA=��BAC=120�㣬
���DBA+��BAD=��BAD+��CAE=60�㣬
���CAE=��ABD��
�ڡ�ADB�͡�CEA�У�$\left\{\begin{array}{l}{��ABD=��CAE}\\{��BDA=��CEA}\\{AB=AC}\end{array}\right.$��
���ADB�ա�CEA��AAS����
��AE=BD����ABD=��CAE��
�ߡ�DBF=60��+��ABD����FAE=60��+��CAE��
���DBF=��FAE��
�ڡ�BDF���AEF�У�$\left\{\begin{array}{l}{BD=AE}\\{��DBF=��EAF}\\{BF=AF}\end{array}\right.$��
���BDF�ա�AEF��
��DF=EF����BFD=��AFE��
�ߡ�BFD+��AFD=60�㣬
���EFA+��AFD=60�㣬
����DFE=60�㣬
���DEF�ǵȱ������Σ�
���DEF���ܳ�Ϊ3DE=3a��
���� �������������ۺ��⣬��Ҫ����ȫ�������ε��ж������ʣ��ȱ������ε����ʣ�������֤��������ȫ�ȵõ�BD=AE��CE=AD�ǽ���Ĺؼ���


 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
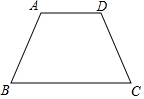 ��ͼ�����ı���ABCD�У�AD��BC��AB=CD=6cm��AD=4cm��BC=10cm�����D�Ķ�����
��ͼ�����ı���ABCD�У�AD��BC��AB=CD=6cm��AD=4cm��BC=10cm�����D�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
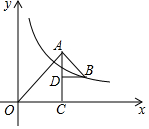 ��ͼ����C��x����������ϣ��ҡ�ACO=90�㣬CO=CA����D�ڱ�AC�ϣ��ڱ�AC���Ҳ�ȡһ��B��ʹ��ADB=90�㣬��BD=DA������������y=$\frac{k}{x}$�ڵ�һ����ͼ����B����S��OAC-S��BAD=5k-2����k��ֵΪ$\frac{4}{9}$��
��ͼ����C��x����������ϣ��ҡ�ACO=90�㣬CO=CA����D�ڱ�AC�ϣ��ڱ�AC���Ҳ�ȡһ��B��ʹ��ADB=90�㣬��BD=DA������������y=$\frac{k}{x}$�ڵ�һ����ͼ����B����S��OAC-S��BAD=5k-2����k��ֵΪ$\frac{4}{9}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
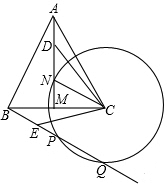 ��ͼ���ڵȱߡ�ABC�У���֪AB=8cm���߶�AMΪBC���ϵ����ߣ���N���߶�AM�ϣ���MN=3cm������D��ֱ��AM���˶�������CD����CBE���ɡ�CAD��ת�õ��ģ��Ե�CΪԲ�ģ���CNΪ�뾶����C��ֱ��BE�ཻ�ڵ�P��Q���㣮
��ͼ���ڵȱߡ�ABC�У���֪AB=8cm���߶�AMΪBC���ϵ����ߣ���N���߶�AM�ϣ���MN=3cm������D��ֱ��AM���˶�������CD����CBE���ɡ�CAD��ת�õ��ģ��Ե�CΪԲ�ģ���CNΪ�뾶����C��ֱ��BE�ཻ�ڵ�P��Q���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com