
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,且与直线
,且与直线![]() 交于
交于![]() .
.
(1)求出点![]() 的坐标
的坐标
(2)当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
(3)点![]() 在x轴上,当△
在x轴上,当△![]() 的周长最短时,求此时点D的坐标
的周长最短时,求此时点D的坐标
(4)在平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,直接写出点
为顶点的四边形是平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)(6,3);(2)![]() ;(3)(0,0);(4)(6,9)或(6,-3)或(-6,3).
;(3)(0,0);(4)(6,9)或(6,-3)或(-6,3).
【解析】
(1)直接联立两直线解析式,即可得到点A的坐标;
(2)直接在图象上找到![]() 时,x的取值范围;
时,x的取值范围;
(3)过点A作![]() 交点为E即可得出点D与点O重合的时候,△
交点为E即可得出点D与点O重合的时候,△![]() 的周长最短,即可得出点D的坐标;
的周长最短,即可得出点D的坐标;
(4)分三种情况考虑:当四边形OAQ1C为平行四边形时;当四边形OQ2AC为平行四边形时;当四边形OACQ3为平行四边形时,分别求出点Q的坐标即可.
(1)联立两直线解析式可得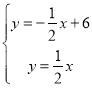
解得:![]()
![]() 点A的坐标为(6,3)
点A的坐标为(6,3)
(2)由点A(6,3)及图象知,当![]() 时,
时,![]()
(3)
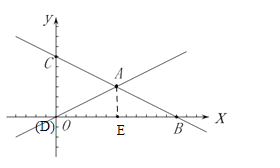
过点A作![]() 交点为E,由图可知点B关于直线AE的对称点为点O
交点为E,由图可知点B关于直线AE的对称点为点O
![]()
![]()
![]() 当点D与点O重合的时候,△
当点D与点O重合的时候,△![]() 的周长最短
的周长最短
即为CO+BC=6+6![]()
此时点D的坐标为(0,0)
(4)存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形
为顶点的四边形是平行四边形
如图所示,分三种情况考虑:
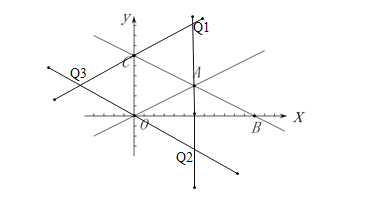
当四边形OAQ1C为平行四边形时,
点Q1的横坐标为6,纵坐标为点C的纵坐标+3=9
![]() Q1的坐标为(6,9)
Q1的坐标为(6,9)
当四边形OQ2AC为平行四边形时,
点Q2的横坐标为6,纵坐标为点A的纵坐标-6=-3
![]() Q2的坐标为(6,-3)
Q2的坐标为(6,-3)
当四边形OACQ3为平行四边形时,
点Q3关于OC的对称点为点A
![]() Q3的坐标为(-6,3)
Q3的坐标为(-6,3)
综上点Q的坐标为:(6,9)或(6,-3)或-6,3).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,0A1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2019的坐标是_____.
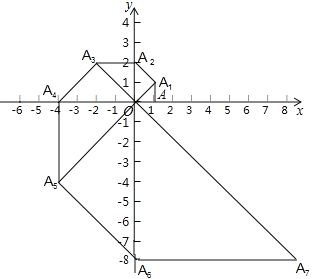
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等腰三角形,AB=AC,点D,E,F分别在AB,BC,AC边上,且BD=CE,BE=CF.
(1)求证:△DEF是等腰三角形;
(2)猜想:当∠A满足什么条件时,△DEF是等边三角形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论.
(3)若∠B=30°,计算S△DAC:S△ABC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于检修部分生产设备,生产能力下降,某工厂现在比原计划平均每天少生产30台机器,现在生产600台机器所需时间与原计划生产900台机器所需时间相同.
问现在平均每天生产多少台机器.
(1)设现在平均每天生产![]() 台机器,则用含
台机器,则用含![]() 的式子表示;
的式子表示;
原计划平均每天生产______台机器,现在生产600台机器所需时间为______天,原计划生产900台机器所需时间为______天;
(2)列出方程,完成本题解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
云阳县多集合生态农业有限公司在2018年种植玉米的平均亩产量为0. 75吨,该公司总结了种植玉米的经验,2019年该公司种植玉米的情况是:种植面积比2018年减少了10%、平均亩产量比2018年增加了0. 2吨,总产量比2018年增加了8. 4吨.
(1)求2018年该公司种植玉米的面积;
(2)若2019年该公司种植玉米的人数比2018年少了12人,人均种植面积比2018年增加了17%,求2019年该公司种植玉米的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com