
【题目】如图,在正方形ABCD中,E,F分别为AD,CD的中点,BF与CE相交于点H,直线EN交CB的延长线于点N,作CM⊥EN于点M,交BF于点G,且CM=CD,有以下结论:①BF⊥CE;②ED=EM;③tan∠ENC=![]() ;④S四边形DEHF=4S△CHF,其中正确结论的个数为()
;④S四边形DEHF=4S△CHF,其中正确结论的个数为()
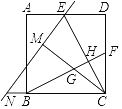
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
①正确.由△CDE≌△BCF,推出∠CBF=∠ECD,由∠ECD+∠ECB=90°,推出∠CBF+∠BCE=90°,推出∠BHC=90°,推出BF⊥CE;
②正确.只要证明Rt△CEM≌Rt△CED即可;
③正确.首先证明NE=NC,设NE=CN=x,EM=DE=AE=a,则CM=CD=2a,在Rt△CNM中,可得(x-a)2+(2a)2=x2,推出![]() 由
由![]() 计算即可;
计算即可;
④正确.易知△CHF∽△CDE,可得![]()
∵四边形ABCD是正方形,
∴![]()
∵![]()
∴DE=CF,
∴△CDE≌△BCF,
∴∠CBF=∠ECD,
∵![]()
∴![]()
∴![]()
∴BF⊥CE,故①正确,
∵![]()
∴Rt△CEM≌Rt△CED,
∴EM=DE,故②正确,
∴∠CED=∠CEM=∠ECN,
∴NE=NC,设NE=CN=x,EM=DE=AE=a,则CM=CD=2a,
在Rt△CNM中,![]()
解得![]()
tan∠ENC![]() 故③正确,
故③正确,
易知△CHF∽△CDE,
∴![]()
∴S四边形DEHF=4S△CHF,故④正确,
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
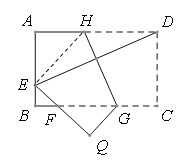
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
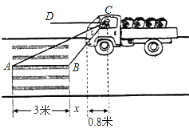
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
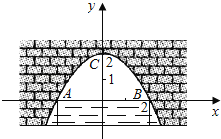
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
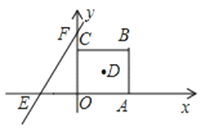
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足![]() ,
,![]()
(1)求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;
(2)直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
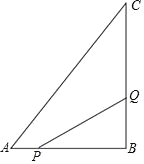
【题目】在△ABC中,AB=10cm,BC=16cm,∠B=90°,点P从点A开始沿着AB边向点B以1cm/s的速度移动(到B停止),点Q从点B开始沿着BC边向点C以2cm/s的速度移动(到C停止).如果P、Q分别从A、B同时出发,经过几秒钟,使△PBQ的面积是△ABC面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
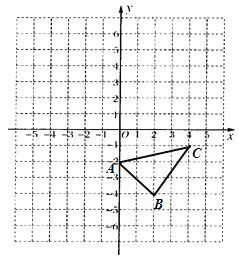
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com