
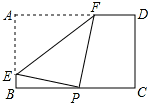
 如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是2≤x≤6.
如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是2≤x≤6. 分析 利用极端原理求解:①BP最小时,F、D重合,由折叠的性质知:AF=PF,在Rt△PFC中,利用勾股定理可求得PC的长,进而可求得BP的值,即BP的最小值;②BP最大时,E、B重合,根据折叠的性质即可得到AB=BP=34,即BP的最大值为4;根据上述两种情况即可得到BP的取值范围.
解答  解:如图:
解:如图:
①当F、D重合时,BP的值最小;
根据折叠的性质知:AF=PF=10;
在Rt△PFC中,PF=10,FC=6,则PC=8;
∴BP=xmin=10-8=2;
②当E、B重合时,BP的值最大;根据折叠的性质即可得到AB=BP=6,即BP的最大值为6.
故答案为:2≤x≤6.
点评 此题主要考查的是图形的翻折变换,正确的判断出x的两种极值下F、E点的位置,是解决此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 如果a<b,那么a-c<b-c | B. | 如果a>b,c>0,那么ac>bc | ||
| C. | 如果m<n,p<0,那么$\frac{m}{p}$>$\frac{n}{p}$ | D. | 如果x>y,z<0,那么xz>yz |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,2cm,4cm | B. | 4cm,5cm,9cm | C. | 5cm,8cm,15cm | D. | 6cm,8cm,9cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在△ABC中,∠BAD=∠CAD,∠B=∠FAC,点F为BC延长线上的一点,且FE平分∠AFD交AB于点E,试判断EF与AD之间的位置关系,并证明.
已知在△ABC中,∠BAD=∠CAD,∠B=∠FAC,点F为BC延长线上的一点,且FE平分∠AFD交AB于点E,试判断EF与AD之间的位置关系,并证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com