
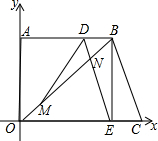
 ��ͼ����ֱ������OABC�У���֪B��C���������ֱ�ΪB��8��6����C��10��0��������M��ԭ��O������OB���������˶����ٶ�Ϊ1��λ/�룻ͬʱ���߶�DE��BC������BA���������˶����ٶ�Ϊ1��λ/�룬��OB�ڵ�N������DM�����˶�ʱ��Ϊt�루0��t��8��
��ͼ����ֱ������OABC�У���֪B��C���������ֱ�ΪB��8��6����C��10��0��������M��ԭ��O������OB���������˶����ٶ�Ϊ1��λ/�룻ͬʱ���߶�DE��BC������BA���������˶����ٶ�Ϊ1��λ/�룬��OB�ڵ�N������DM�����˶�ʱ��Ϊt�루0��t��8������ ��1����DM��OA����$\frac{DB}{BA}$=$\frac{BM}{OB}$���г����̼��ɽ�����⣮
��2�������OB=OC=10������֪BM=OE=10-t����BD=OM=t���ҡ�DBM=��MOE������֤�á�BDM�ա�OME���������ε������ת��Ϊ��OBC��������������ε�����Ƕ�ֵ����OCΪ�ס�OAΪ�ߣ�������á�OCB�������Ҳ���������ֵ�Ĵ�С��
��3������������BD=BM����DM=DB����MD=BM���ۼ��ɣ�
��� �⣺��1����Rt��ABO�У���OA=6��AB=8��
��BO=$\sqrt{O{A}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10��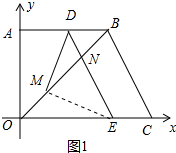
��DM��OA��
��$\frac{DB}{BA}$=$\frac{BM}{OB}$��
��$\frac{t}{8}$=$\frac{10-t}{10}$��
��t=$\frac{40}{9}$��
��t=$\frac{40}{9}$��ʱ��DM��OA��
��2����AB��OC��
���DBM=��MOE
��BD=OM=t��BM=EO=10-t��
���ڡ�BDM�͡�OME�У�
$\left\{\begin{array}{l}{BD=OM}\\{��DBM=��MOE}\\{BM=OE}\end{array}\right.$
���BDM�ա�OME��
�Ӷ������MECBD���������������OBC��������������һ����ֵ��
SMECBD=S��OCB=$\frac{1}{2}$��10��6=30��
��3���ٵ�BD=BMʱ��t=10-t��
���t=5��
�ڵ�DM=DBʱ����ͼ3�У���DG��OB��G��
��DM=DB��DG��BM��
��MG=BG=$\frac{1}{2}$��10-t����
��cos��DBG=$\frac{BG}{BD}=\frac{4}{5}$��
��$\frac{\frac{1}{2}��10-t��}{t}$=$\frac{4}{5}$��
���t=$\frac{50}{13}$��
�۵�DM=BMʱ����ͼ3�У���MG��BD��G��
����cos��MBG=$\frac{BG}{BM}$=$\frac{4}{5}$��
��$\frac{\frac{1}{2}t}{10-t}$=$\frac{4}{5}$��
��t=$\frac{80}{13}$��
����������t=5��$\frac{50}{13}$��$\frac{80}{13}$��ʱ����BDM�ǵ��������Σ�
���� ���⿼��ֱ�����ε����ʡ�ȫ�������ε��ж������ʡ�ͼ������������������ε��ж���ƽ���߷��߶γɱ���������֪ʶ������Ĺؼ������Ӧ����Щ֪ʶ������⣬ѧ��������ۣ�ע�ⲻ��©�⣬�����п�ѹ���⣮


 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸���ABC�������������ߵĽ��㣩��
��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸���ABC�������������ߵĽ��㣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ����в��ϣ�Ȼ��ش����⣮
�Ķ����в��ϣ�Ȼ��ش����⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵĶ��㣨��˵�B��C���غϣ�������D��ֱ��y=-x+b������OAB�ڵ�E��
��ͼ��ʾ���ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵĶ��㣨��˵�B��C���غϣ�������D��ֱ��y=-x+b������OAB�ڵ�E���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com