
���� ��1��ֱ�Ӹ��ݸ��ʹ�ʽ���㣻
��2����������״ͼչʾ���˵���ָ֮�͵�����36�ֵȿ��ܵĽ���������ҳ���Ϊ5���Ϊ8�Ľ������Ȼ����ݸ��ʹ�ʽ�������˻�ʤ�ĸ��ʣ��ٱȽϸ��ʵĴ�С���ɣ�
��� �⣺��1����ָһ�ι���6�ֿ��ܣ���С����2����ָ�ĸ���=$\frac{1}{6}$��
��2������״ͼΪ��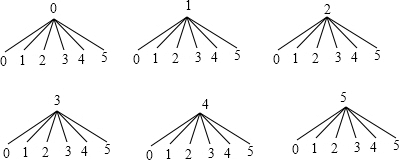
���˵���ָ֮����36�ֵȿ��ܵĽ���������к�Ϊ5ռ6�֣���Ϊ8ռ3�֣�
��ְֻ�ʤ�ĸ���Ϊ��$\frac{6}{36}$=$\frac{1}{6}$��
С����ʤ�ĸ���Ϊ��$\frac{3}{36}$=$\frac{1}{12}$��
�ʰְֻ�ʤ�Ŀ����Ը���
���� ���⿼�����б�������״ͼ���������б�������״ͼ��չʾ���п��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ����ݸ��ʹ�ʽ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 0 | C�� | 1 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | С�ŵķ���С�����ˮƽû��С���ȶ� | |
| B�� | С�ŵķ���С�����ˮƽ��С���ȶ� | |
| C�� | С���ķ�������ˮƽ��С���ȶ� | |
| D�� | �����ܳɼ���ͬ��С�ź�С������ȶ�����ͬ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
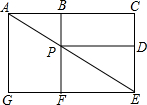 ��ͼ��һֻС��������A�㲻�ظ��ľ���ͼ�е�ÿһ�����ÿһ���߶ζ����յ���Ŀ�ĵ�E��������ֻС������A��P��E���ߵĸ����ǣ�������
��ͼ��һֻС��������A�㲻�ظ��ľ���ͼ�е�ÿһ�����ÿһ���߶ζ����յ���Ŀ�ĵ�E��������ֻС������A��P��E���ߵĸ����ǣ�������| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{1}{9}$ | D�� | $\frac{1}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
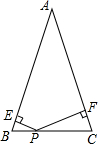 ��ͼ����֪����������ABC�У�AB=AC=10cm����A=30�㣬P��BC��һ�㣬PE��AB��PF��AC������ֱ�Ϊ��E��F����PE+PF=��������
��ͼ����֪����������ABC�У�AB=AC=10cm����A=30�㣬P��BC��һ�㣬PE��AB��PF��AC������ֱ�Ϊ��E��F����PE+PF=��������| A�� | 2.5cm | B�� | 2$\sqrt{2}$cm | C�� | 5cm | D�� | 2$\sqrt{3}$cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 23��32 | B�� | m2n��$-\frac{1}{2}m{n^2}$ | C�� | 2��R���2R | D�� | -x2y��2yx2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com