
【题目】合肥百货大厦某店卖一种狗宝宝布娃娃纪念品,已知成批购进时单价为4元,根据市场调查,销售量与销售单价在一段时间内满足如下关系:单价为10元时销售量为300枚,而单价每降低1元,就可多售出5枚,那么求可获得最大利润为__元.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
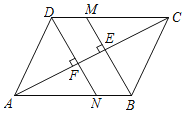
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C的坐标分别为(a,0),(0,b),点B在第一象限内,且a,b满足|a3﹣64|+![]() =0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
=0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).

(1)求点B的坐标;
(2)当点P移动4秒时,求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,请直接写出点P移动的时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)己知2a-1的平方根是土3,3a+b-1的平方根是土4,c是![]() 的整数部分,求a+2b+c的算术平方根.
的整数部分,求a+2b+c的算术平方根.
(2)已知在△ABC中,AB=10,BC=21,AC=17,则△ABC面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】最近雾霾天气频繁,使得空气净化器得以畅销.某商场代理销售某种空气净化器,其进价是500元/台,经过市场销售后发现,当售价是1000元/台时,每月可售出50台,且售价每降低20元,每月就可多售出5台.若供货商规定这种空气净化器售价不能低于600元/台,代理销售商每月要完成不低于60台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式,并求出自变量x的取值范围.
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×![]() ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .

(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少?
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com