
【题目】如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
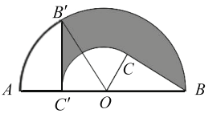
【题目】如图,![]() 为半圆内一点,
为半圆内一点,![]() 为圆心,直径
为圆心,直径![]() 长为
长为![]() ,
,![]() ,
,![]() ,将
,将![]() 绕圆心
绕圆心![]() 逆时针旋转至
逆时针旋转至![]() ,点
,点![]() 在
在![]() 上,则边
上,则边![]() 扫过区域(图中阴影部分)的面积为__________
扫过区域(图中阴影部分)的面积为__________![]() .(结果保留
.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某影院共有25排座位,第1排有11个座位数,从第2排开始,每一排都比前一排增加m个座位.
(1)请你在下表的空格里填写一个适当的代数式:
第1排的座位数 | 第2排的座位数 | 第3排的座位数 | … | 第n排的座位数 |
11 | 11+m | 11+2m | … | ______ |
(2)已知第18排座位数是第4排座位数的2倍,那么影院共有多少个座位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的结论有________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点O,D分别为AB,BC的中点,连接OD,作⊙O与AC相切于点E,在AC边上取一点F,使DF=DO,连接DF.
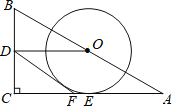
(1)判断直线DF与⊙O的位置关系,并说明理由;
(2)当∠A=30°,CF![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;
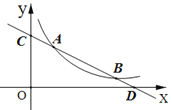
(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形AOBC中,OB=8,OA=4.分别以OB,OA所在直线为x轴,y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
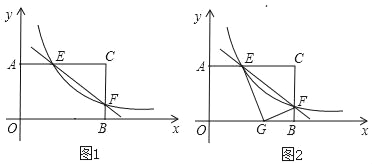
(1)当点F运动到边BC的中点时,求点E的坐标;
(2)连接EF、AB,求证:EF∥AB;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求此时反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
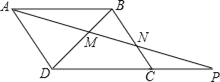
【题目】如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)图中相似三角形共有_____对;
(2)证明:AM2=MNMP;
(3)若AD=6,DC:CP=2:1,求BN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com