
【题目】观察下列多面体,并把下表补充完整.
名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
图形 |
|
|
|
|
顶点数 | 6 | 10 | 12 | |
棱数 | 9 | 12 | ||
面数 | 5 | 8 |
观察上表中的结果,你能发现![]() 、
、![]() 、
、![]() 之间有什么关系吗?请写出关系式
之间有什么关系吗?请写出关系式
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣ ![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣ ![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.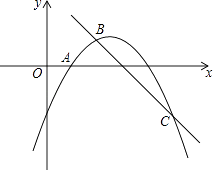
(1)求二次函数y=﹣ ![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1 , B2 , B3 , …,则B2017的坐标为( )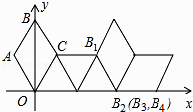
A.(1345,0)
B.(1345.5, ![]() )
)
C.(1345, ![]() )
)
D.(1345.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
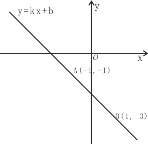
【题目】已知一次函数y=kx+b的图象经过点A(1,1)和点B(1,3).求:
(1)求一次函数的表达式;
(2)求直线AB与坐标轴围成的三角形的面积;
(3)请在x轴上找到一点P,使得PA+PB最小,并求出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:

小凯的作法如下:
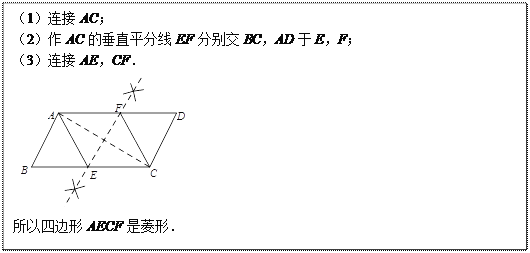
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一堂公开课,老师在黑板上写了两个代数式![]() 与
与![]() ,让大家相互之间用这两个代数式出题考对方.
,让大家相互之间用这两个代数式出题考对方.
(1)小明给小红出的题为:若代数式![]() 与
与![]() 的值多1,求3a2﹣2(2a2+a)+2(a2﹣3a)的值;
的值多1,求3a2﹣2(2a2+a)+2(a2﹣3a)的值;
(2)小红想为难一下小明,她给小明出的题为:已知a为负数,比较代数式![]() 与
与![]() 的大小,请你帮小明作出解答.
的大小,请你帮小明作出解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: ![]() .我们称使得
.我们称使得![]() 成立的一对数
成立的一对数![]() ,
, ![]() 为“相伴数对”,记为
为“相伴数对”,记为![]() .
.
(1)若![]() 是“相伴数对”,求
是“相伴数对”,求![]() 的值;
的值;
(2)写出一个“相伴数对” ![]() ,其中
,其中![]() 且
且![]() ;
;
(3)若![]() 是“相伴数对”,求代数式
是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
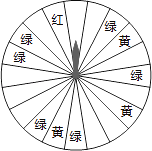
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com