
【题目】(1)机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?
(2)某蔬菜公司的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司的加工生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案:
方案一:将蔬菜全部进行粗加工.
方案二:尽可能多地对蔬菜进行精加工,没来得及进行加工的蔬菜,在市场上直接销售.
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为哪种方案获利最多?为什么?
【答案】(1)需安排25名工人加工大齿轮,安排60名工人加工小齿轮;(2)该公司可以粗加工这种食品80吨,精加工这种食品60吨,可获得最高利润为810000元.
【解析】
(1)设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,根据平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,可列成方程组求解.
(2)方案一:直接用算术方法计算:粗加工的利润×吨数;方案二:首先根据每天精加工的吨数以及天数的限制,知精加工了15×6=90吨,还有50吨直接销售;方案三:设精加工x天,则粗加工(15﹣x)天,根据加工的总吨数为140吨列方程求得x的值,然后可求得获得的利润.
(2)设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,根据题意得:
![]()
解得:![]() .
.
答:需安排25名工人加工大齿轮,安排60名工人加工小齿轮.
(2)方案一:∵4500×140=630000(元),∴将食品全部进行粗加工后销售,则可获利润630000元;
方案二:15×6×7500+(140﹣15×6)×1000=725000(元),∴将食品尽可能多的进行精加工,没来得及加工的在市场上直接销售,则可获利润725000元;
方案三:设精加工x天,则粗加工(15﹣x)天.
根据题意得:6x+16(15﹣x)=140,解得:x=10,所以精加工的吨数=6×10=60,16×5=80吨.
这时利润为:80×4500+60×7500=810000(元)
答:该公司可以粗加工这种食品80吨,精加工这种食品60吨,可获得最高利润为810000元.


科目:初中数学 来源: 题型:
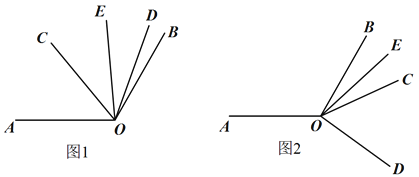
【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图1.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图2,当∠COD在∠AOB的外部时,(1)中∠AOC与∠DOE的数量关系还成立吗?若成立,请推导出∠AOC与∠DOE的度数之间的关系;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=![]() ∠AOE,求∠BOD的度数?
∠AOE,求∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的两边BC,AB分别在平面直角坐标系的x轴、y轴的正半轴上,正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形,已知AC=3 ![]() ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( ) 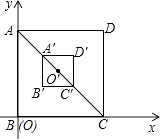
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
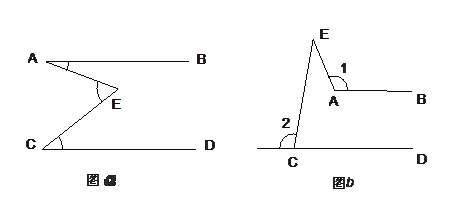
(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com