
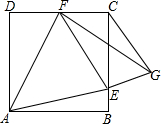
 如图,在正方形ABCD中,E、F分别是BC、DC上的两点,若EF=BE+DF.
如图,在正方形ABCD中,E、F分别是BC、DC上的两点,若EF=BE+DF.| 2 |
| 2 |
| 2 |
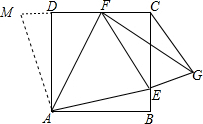 (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,
|
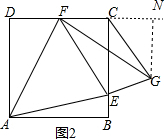
|
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 某中学老年活动中心排练一个扇子舞蹈,需要手工制作一个周长为120cm的扇子(如图①所示)
某中学老年活动中心排练一个扇子舞蹈,需要手工制作一个周长为120cm的扇子(如图①所示)查看答案和解析>>
科目:初中数学 来源: 题型:
| a+1 |
| a-1 |
| a |
| a2-2a+1 |
| 1 |
| a |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
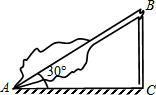 如图,记得今年上半年一次大风把学校门口对面一棵大树在离地面B点处的拦腰刮断,折断部分AB与地面恰好形成30°的夹角,树顶端着地点A到树根部C的距离为6米,请同学们计算这棵树的原来的高度是
如图,记得今年上半年一次大风把学校门口对面一棵大树在离地面B点处的拦腰刮断,折断部分AB与地面恰好形成30°的夹角,树顶端着地点A到树根部C的距离为6米,请同学们计算这棵树的原来的高度是查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 5 |
| 14 |
| 4 |
| 25 |
| 1 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com