

图13-3-20
①△DAC______△EAC;
②DC与CE的大小关系是____________;
③∠D与∠CEB的关系是____________.
(2)用你得到的结论解决下面的问题:
在四边形ABCD中,已知AB=a,AD=b,且BC=DC,对角线AC平分∠BAD.问a与b大小符合什么条件时,有∠D+∠B=180°?请画图并证明你的结论.
|
思路解析:翻折图形是全等形.从图形可以看出,若以C为圆心,CE为半径画弧,弧与AB的交点有两个,所以应注意分类讨论.
答案:(1)①≌ ②相等 ③互补 (2)结论:分两种情况:①当a≠b时,都有∠D+∠ABC=180°. 证明:(如下图)在AB上截取AE=AD.
由(1)得∠D+∠ECB=180°,EC=DC. ∵BC=CD,∴EC=BC. 作CH⊥BE,垂足为H. 在Rt△CHE与Rt△CHB中, ∴Rt△CHE≌Rt△CHB. ∴∠CEB=∠B. ∴∠D+∠ABC=180°. ②当a=b,且∠D=90°时,有∠D+∠ABC=180°. 证明:如下图.∵AD=AB,BC=CD,AC=AC,
∴△ADC≌△ABC. ∴∠D=∠ABC=90°. ∴∠D+∠ABC=180°. |


科目:初中数学 来源: 题型:
问题:如图(12),在菱形![]() 和菱形
和菱形![]() 中,点
中,点![]() 在同一条直线上,
在同一条直线上,![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .探究
.探究![]() 与
与![]() 的位置关系及
的位置关系及![]() 的值.小聪同学的思路是:延长
的值.小聪同学的思路是:延长![]() 交
交![]() 于点
于点![]() ,构造全等三角形,经过推理使问题得到解决.
,构造全等三角形,经过推理使问题得到解决.
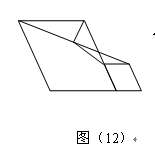
请你参考小聪同学的思路,探究并解决下列问题:
1.若图(12)中![]() ,写出线段
,写出线段![]() 与
与![]() 的位置关系及
的位置关系及![]() 的值,并说明理由;
的值,并说明理由;
2.将图(12)中的菱形![]() 绕点
绕点![]() 顺时针旋转,使菱形
顺时针旋转,使菱形![]() 的对角线
的对角线![]() 恰好与菱形
恰好与菱形![]() 的边
的边![]() 在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
在同一条直线上,原问题中的其他条件不变(如图13).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.
3.若图(12)中![]() ,将菱形
,将菱形![]() 绕点
绕点![]() 顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出
顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
解:(1)线段![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
 处观测到河对岸水边有一点
处观测到河对岸水边有一点 ,测得
,测得 在
在 北偏西
北偏西 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达 处,测得
处,测得 在
在 北偏西
北偏西 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈ ,sin31°≈
,sin31°≈ )
) 
查看答案和解析>>
科目:初中数学 来源:2011届河北省廊坊市安次区初三第一次模拟考试数学试题 题型:填空题
如图13,在等腰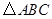 中,
中, ,
, ,点
,点 从点
从点 开始沿
开始沿 边以每秒1
边以每秒1 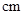 的速度向点
的速度向点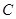 运动,点
运动,点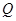 从点
从点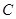 开始沿
开始沿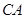 边以每秒2
边以每秒2 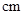 的速度向点
的速度向点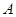 运动,
运动,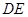 保持垂直平分
保持垂直平分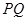 ,且交
,且交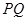 于点
于点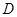 ,交
,交 于点
于点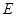 .点
.点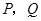 分别从
分别从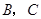 两点同时出发,当点
两点同时出发,当点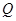 运动到点
运动到点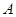 时,点
时,点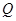 、
、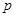 停止运动,设它们运动的时间为
停止运动,设它们运动的时间为 .
.
(1)当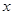 = 秒时,射线
= 秒时,射线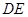 经过点
经过点 ;
;
(2)当点 运动时,设四边形
运动时,设四边形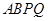 的面积为
的面积为 ,求
,求 与
与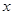 的函数关系式(不用写出自变量取值范围);
的函数关系式(不用写出自变量取值范围);
(3)当点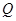 运动时,是否存在以
运动时,是否存在以 为顶点的三角形与△
为顶点的三角形与△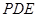 相似?若存在,求出
相似?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:11.2三角形全等的判定同步练习数学卷 题型:填空题
如图13,∠E=∠F=900,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是 (填序号).
查看答案和解析>>
科目:初中数学 来源:2011年湖北省武汉市青山区初一上学期数学期末考试数学卷 题型:解答题
如图13,已知EF⊥BC,∠1=∠C,∠2+∠3=180°. 试说明直线AD与BC垂直.(请在下面的解答过程的空格内填空或在括号内填写理由).

理由:
∵ ∠1=∠C, ( 已知 )
∴ ∥ ,( )
∴ ∠2= . ( )
又∵ ∠2+∠3=180°,( 已知 )
∴ ∠3+ =180°.( 等量代换 )
∴ ∥ , ( )
∴ ∠ADC=∠EFC. ( )
∵ EF⊥BC, ( 已知 )
∴ ∠EFC=90°,
∴ ∠ADC=90°,
∴ ⊥ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com