
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,进市场调查,甲种花卉的种植费用y(元)与种植面积xm2之间的函数关系如图所示,乙种花卉的种植费用为100元/m2.
(1)请直接写出当0≤x≤300和x>300时,y与x的函数关系式;

(2)广场上甲、乙两种花卉的种植面积共1200m2,如果甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
(3)在(2)的条件下,若种植总费用不小于123000元,求出甲种花卉种植面积的范围是多少?
【答案】(1) 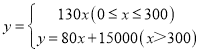 ;(2) 应该分配甲、乙两种花卉的种植面积分别是800m2 和400m2,才能使种植总费用最少,最少总费用为119000元;(3) 甲种花卉种植面积的范围是200≤a≤600
;(2) 应该分配甲、乙两种花卉的种植面积分别是800m2 和400m2,才能使种植总费用最少,最少总费用为119000元;(3) 甲种花卉种植面积的范围是200≤a≤600
【解析】
(1)一次函数是分段函数,分为2段利用代入系数法可求得;
(2)设甲种花卉种植面积为am2,总费用为W,分2段写出a关于W的一次函数,然后分别讨论这2段函数的最小值,最后在这2个最小值中选取一个最小的值;
(3)相当于添加了一个关于a的不等式,解得a的取值范围和前2问的范围相结合即a最终的取值范围.
解:(1)当0≤x≤300是,设y=kx,根据题意得300k=39000,
解得k=130;
∴y=130x;
当x>300时,设y=k1x+b,
根据题意得,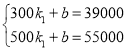 ,
,
解得![]() ,
,
∴y=80x+15000.
∴y=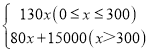 ;
;
(2)设甲种花卉种植面积为am2,则乙种花卉种植面积为(1200﹣a)m2.
∴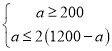 ,
,
∴200≤a≤800,
当200≤a≤300时,W1=130a+100(1200﹣a)=30a+120000.
当a=200 时.Wmin=126000 元
当300<a≤800时,W2=80a+15000+100(1200﹣a)=135000﹣20a.
当a=800时,Wmin=119000 元
∵119000<126000
∴当a=800时,总费用最少,最少总费用为119000元.
此时乙种花卉种植面积为1200﹣800=400m2.
答:应该分配甲、乙两种花卉的种植面积分别是800m2 和400m2,才能使种植总费用最少,最少总费用为119000元.
(3)根据题意得135000﹣20a≥123000,
解得a≤600.
∴甲种花卉种植面积的范围是200≤a≤600.


科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() ;当自变量
;当自变量![]() 的值为
的值为![]() 或
或![]() 时,函数值都为
时,函数值都为![]() .探究过程如下,请补充完整.
.探究过程如下,请补充完整.
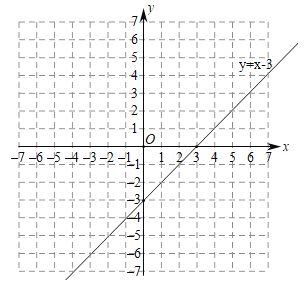
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的--条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有三个交点,则
有三个交点,则![]() ;
;
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]()
![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=![]() (m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式![]() >kx+b的解集.
>kx+b的解集.
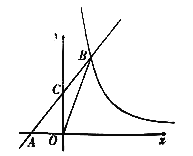
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图样中,产生的有害垃圾C所对应的圆心角 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设该城市每月产生的生活垃圾为1000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用10个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要______个小立方体,王亮所搭几何体的表面积为______.
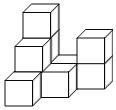
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图,点
的图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,
位于第一象限的图象上,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都是直角顶点在抛物线上的等腰直角三角形,则
都是直角顶点在抛物线上的等腰直角三角形,则![]() 的斜边长为________.
的斜边长为________.
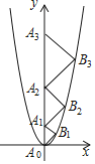
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com