
【题目】定义:在平面直角坐标系中,一个图形先向右平移a个单位,再绕原点按顺时针方向旋转θ角度,这样的图形运动叫作图形的γ(a,θ)变换.
如图,等边△ABC的边长为1,点A在第一象限,点B与原点O重合,点C在x轴的正半轴上.△A1B1C1就是△ABC经γ(1,180°)变换后所得的图形.
若△ABC经γ(1,180°)变换后得△A1B1C1,△A1B1C1经γ(2,180°)变换后得△A2B2C2,△A2B2C2经γ(3,180°)变换后得△A3B3C3,依此类推……
△An﹣1Bn﹣1Cn﹣1经γ(n,180°)变换后得△AnBnCn,则点A1的坐标是__,点A2018的坐标是 .

【答案】(﹣![]() ,﹣
,﹣![]() ),(﹣
),(﹣![]() ,
,![]() ).
).
【解析】
分析图形的γ(a,θ)变换的定义可知:对图形γ(n,180°)变换,就是先进行向右平移n个单位变换,再进行关于原点作中心对称变换.向右平移n个单位变换就是横坐标加n,纵坐标不变,关于原点作中心对称变换就是横纵坐标都变为相反数.写出几次变换后的坐标可以发现其中规律.
根据图形的γ(a,θ)变换的定义可知:
对图形γ(n,180°)变换,就是先进行向右平移n个单位变换,再进行关于原点作中心对称变换.
△ABC经γ(1,180°)变换后得△A1B1C1,A1 坐标(﹣![]() ,﹣
,﹣![]() )
)
△A1B1C1经γ(2,180°)变换后得△A2B2C2,A2坐标(﹣![]() ,
,![]() )
)
△A2B2C2经γ(3,180°)变换后得△A3B3C3,A3坐标(﹣![]() ,﹣
,﹣![]() )
)
△A3B3C3经γ(4,180°)变换后得△A4B4C4,A4坐标(﹣![]() ,
,![]() )
)
依此类推横坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…
可以发现规律:An横坐标当n为奇数则横坐标为![]() ,n为偶数时,横坐标为
,n为偶数时,横坐标为![]() ,纵坐标为(-1)n
,纵坐标为(-1)n![]()
当n=2018时,有2018÷3=672余2
所以,A2018横坐标是﹣![]() ,纵坐标为
,纵坐标为![]()
故答案为:(﹣![]() ,﹣
,﹣![]() ),(﹣
),(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】一组连续奇数按如图方式排列,请你解决下列问题:

![]() 第
第![]() 行最后一个数字是___________,在第
行最后一个数字是___________,在第![]() 行第
行第![]() 列的数字是_______________
列的数字是_______________
![]() 请用含
请用含![]() 的代数式表示第
的代数式表示第![]() 行的第
行的第![]() 个数字和最后一个数字;
个数字和最后一个数字;
![]() 现用一个正方形框去围出相邻两行中的
现用一个正方形框去围出相邻两行中的![]() 个数字(例如:第
个数字(例如:第![]() 行和第
行和第![]() 行的
行的![]() ),请问能否在第
),请问能否在第![]() 行和第
行和第![]() 行中求出
行中求出![]() 个数字的和是
个数字的和是![]() ?若能,请求出这
?若能,请求出这![]() 个数字;若不能,请说明理由.
个数字;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
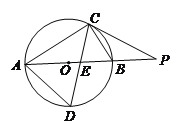
【题目】如图,⊙O的直径AB为2cm,弦BC为1cm,∠ACB的平分线与⊙O交于点D,与AB交于点E,P为AB延长线上一点,连接PC,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=45°,若BD=2,CD=3,AD⊥BC于D,将△ABD沿AB所在的直线折叠,使点D落在点E处;将△ACD沿AC所在的直线折叠,使点D落在点F处,分别延长EB、FC使其交于点M.
(1)判断四边形AEMF的形状,并给予证明.
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求四边形AEMF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
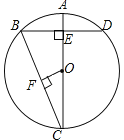
A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段![]() 和线段
和线段![]() .
.

(1)按要求作图(保留作围痕迹,不写作法);
延长线段![]() 至点
至点![]() ,使
,使![]() ,反向延长线段
,反向延长线段![]() 至点
至点![]() ,使
,使![]() ;
;
(2)如果![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间接到一批限期(可以提前)完成的零件加工任务.如果每天加工150个,则恰好按期完成;如果每天加工200个,则可比原计划提前5天完成.
(1)求这批零件的个数;
(2)车间按每天加工200个零件的速度加工了![]() 个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求
个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”.为保护生态环境,A、B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:

(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元?
(2)在人均支出费用不变的情况下,为节约开支,两村准备协调40人共同清理养鱼网箱和捕鱼网箱.要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1) 分别写出当0≤x≤100和x>100时,y与x的函数关系式
(2) 利用函数关系式,说明电力公司采取的收费标准
(3) 若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com