
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
【答案】
(1)
解:把点A(4,0),B(1,3)代入抛物线y=ax2+bx中,
得 ![]() 解得:
解得: ![]() ,
,
∴抛物线表达式为:y=﹣x2+4x;
(2)
解:点C的坐标为(3,3),
又∵点B的坐标为(1,3),
∴BC=2,
∴S△ABC= ![]() ×2×3=3;
×2×3=3;
(3)
解:过P点作PD⊥BH交BH于点D,
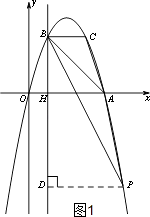
设点P(m,﹣m2+4m),
根据题意,得:BH=AH=3,HD=m2﹣4m,PD=m﹣1,
∴S△ABP=S△ABH+S四边形HAPD﹣S△BPD,
6= ![]() ×3×3+
×3×3+ ![]() (3+m﹣1)(m2﹣4m)﹣
(3+m﹣1)(m2﹣4m)﹣ ![]() (m﹣1)(3+m2﹣4m),
(m﹣1)(3+m2﹣4m),
∴3m2﹣15m=0,
m1=0(舍去),m2=5,
∴点P坐标为(5,﹣5).
(4)
解:以点C、M、N为顶点的三角形为等腰直角三角形时,分三类情况讨论:
①以点M为直角顶点且M在x轴上方时,如图2,CM=MN,∠CMN=90°,

则△CBM≌△MHN,
∴BC=MH=2,BM=HN=3﹣2=1,
∴M(1,2),N(2,0),
由勾股定理得:MC= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
②以点M为直角顶点且M在x轴下方时,如图3,作辅助线,构建如图所示的两直角三角形:Rt△NEM和Rt△MDC,
得Rt△NEM≌Rt△MDC,
∴EM=CD=5,MD=NE=2,
由勾股定理得:CM= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;

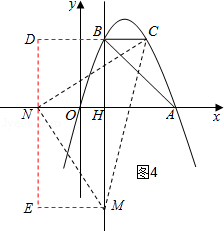
③以点N为直角顶点且N在y轴左侧时,如图4,CN=MN,∠MNC=90°,作辅助线,
同理得:CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =17;
=17;
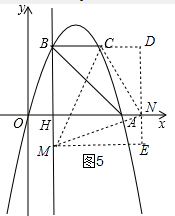
④以点N为直角顶点且N在y轴右侧时,作辅助线,如图5,同理得:CN= ![]() =
= ![]() ,
,
∴S△CMN= ![]() ×
× ![]() ×
× ![]() =5;
=5;
⑤以C为直角顶点时,不能构成满足条件的等腰直角三角形,如图6;
综上所述:△CMN的面积为: ![]() 或
或 ![]() 或17或5.
或17或5.

【解析】(1)利用待定系数法求二次函数的表达式;(2)根据二次函数的对称轴x=2写出点C的坐标为(3,3),根据面积公式求△ABC的面积;(3)因为点P是抛物线上一动点,且位于第四象限,设出点P的坐标(m,﹣m2+4m),利用差表示△ABP的面积,列式计算求出m的值,写出点P的坐标;(4)分别以点C、M、N为直角顶点分三类进行讨论,利用全等三角形和勾股定理求CM或CN的长,利用面积公式进行计算.


科目:初中数学 来源: 题型:
【题目】一副三角板按如图所示叠放在一起,若固定![]() ,将
,将![]() 绕着公共顶点
绕着公共顶点![]() ,按顺时针方向旋转
,按顺时针方向旋转![]() 度
度![]() ,当
,当![]() 的一边与
的一边与![]() 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角![]() 的度数为_________________。
的度数为_________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B( ![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 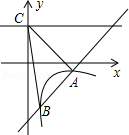
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
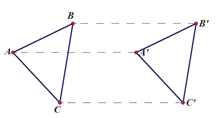
【题目】如图所示,将△ABC平移到△A′B′C′的位置,连接BB′,AA′,CC′,平移的方向是点______到点________的方向,平移的距离是线段______的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,
将若干个点摆成三角形图案,每条边(包括两个端点)有n(n是正整数且n>1)个点,相应的图案中总的点数记为an , 则 ![]() +
+ ![]() +…+
+…+ ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;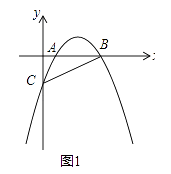
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;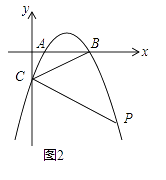
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 ![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.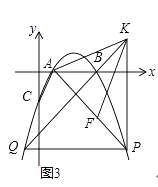
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com