
【题目】如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )
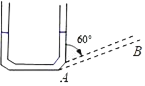
A. 4cmB. 2![]() cmC. 3cmD. 8cm
cmC. 3cmD. 8cm
【答案】A
【解析】
AB中水柱的长度为AC,CH为此时水柱的高,设CH=x,竖直放置时短软管的底面积为S,易得AC=2CH=2x,细管绕A处顺时针方向旋转60°到AB位置时,底面积为2S,利用水的体积不变得到xS+x2S=6S+6S,然后求出x后计算出AC即可.
解:AB中水柱的长度为AC,CH为此时水柱的高,设CH=x,竖直放置时短软管的底面积为S,
∵∠BAH=90°﹣60°=30°,
∴AC=2CH=2x,
∴细管绕A处顺时针方向旋转60°到AB位置时,底面积为2S,
∵xS+x2S=6S+6S,解得x=4,
∴CH=x=4,
即此时“U”形装置左边细管内水柱的高度约为4cm.
故选:A.


科目:初中数学 来源: 题型:
【题目】为了测量白塔的高度AB,在D处用高为1.5米的测角仪 CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB.(参考数据sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数)
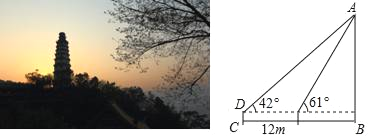
查看答案和解析>>
科目:初中数学 来源: 题型:
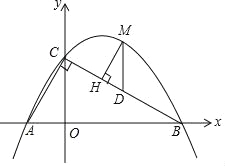
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点.
经过A,B两点.
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饭店推出一种早点套餐,试销一段时间后发现,每份套餐的成本为5元,若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份,该店每天固定支出费用为600元![]() 不含套餐成本
不含套餐成本![]() 为了便于结算,每份套餐的售价取整数,设每份套餐的售价为
为了便于结算,每份套餐的售价取整数,设每份套餐的售价为![]() 元,该店日销售利润为y元
元,该店日销售利润为y元![]() 日销售利润
日销售利润![]() 每天的销售额
每天的销售额![]() 套餐成本
套餐成本![]() 每天固定支出
每天固定支出![]()
![]() 求y与x的函数关系式并写出自变量的取值范围.
求y与x的函数关系式并写出自变量的取值范围.
![]() 该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
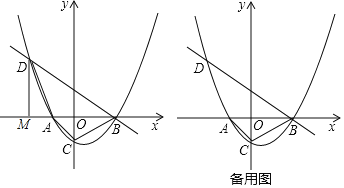
【题目】如图,已知抛物线![]() (k为常数,且
(k为常数,且![]() )与x轴从左至右依次交于A,B两点,与y轴交于点C过点B的直线
)与x轴从左至右依次交于A,B两点,与y轴交于点C过点B的直线![]() 与抛物线的另一交点为D.
与抛物线的另一交点为D.
![]() 若点D的横坐标为
若点D的横坐标为![]() ,求抛物线的函数表达式;
,求抛物线的函数表达式;
![]() 过D点向x轴作垂线,垂足为点M,连结AD,若
过D点向x轴作垂线,垂足为点M,连结AD,若![]() ,求点D的坐标;
,求点D的坐标;
![]() 若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与
若在第一象限的抛物线上有一点P,使得以点A,B,P为顶点的三角形与![]() 相似,请直接写出
相似,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在足球场上练习足球传球,足球从一个人传到另一个人记为踢一次.如果从小强开始踢,经过两次踢球后,足球踢到小华处的概率是多少?经过三次踢球后,足球踢回到小强处的概率呢?(列表或画树形图或列举)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个透明的布袋里装有2个红球,![]() 个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为
个白球,它们除颜色外其余都相同,已知任意摸出1个球是红球的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)先任意摸出1个球,记下颜色后不放回,搅匀,再摸出一个球,请利用画树状图或列表的方法求出连续两次都摸出红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3;③a+b+c<0;④当x>1时,y随x的增大而增大,正确的是( )
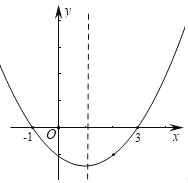
A. ①③B. ②④C. ①②④D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com